Chapitre 4 Visualisation avec ggplot2

Il est souvent nécessaire d’utiliser des techniques de visualisation au cours des différentes étapes d’un projet en science des données. Un des avantages de R est qu’il est relativement simple de mettre en œuvre tous les types de graphes généralement utilisés. Dans cette partie, nous présentons tout d’abord les fonctions classiques qui permettent de tracer des figures. Nous proposons ensuite une introduction aux graphes ggplot qui sont de plus en plus utilisés pour faire de la visualisation.

4.1 Fonctions graphiques conventionnelles

Pour commencer il est intéressant d’examiner quelques exemples de représentations graphiques construits avec R. On peut les obtenir à l’aide de la fonction demo.

demo(graphics)

4.1.1 La fonction plot

C’est une fonction générique que l’on peut utiliser pour représenter différents types de données. L’utilisation standard consiste à visualiser une variable y en fonction d’une variable x. On peut par exemple obtenir le graphe de la fonction \(x\mapsto \sin(2\pi x)\) sur \([0,1]\), à l’aide de

x <- seq(-2*pi,2*pi,by=0.05)
y <- sin(x)
plot(x,y) #points (par défaut)

plot(x,y,type="l") #représentation sous forme de ligne

Nous proposons des exemples de représentations de variables quantitatives et qualitatives à l’aide du jeu de données ozone.txt que l’on importe avec

ozone <- read.table("data/ozone.txt")
summary(ozone)
     maxO3              T9             T12       
 Min.   : 42.00   Min.   :11.30   Min.   :14.00  
 1st Qu.: 70.75   1st Qu.:16.20   1st Qu.:18.60  
 Median : 81.50   Median :17.80   Median :20.55  
 Mean   : 90.30   Mean   :18.36   Mean   :21.53  
 3rd Qu.:106.00   3rd Qu.:19.93   3rd Qu.:23.55  
 Max.   :166.00   Max.   :27.00   Max.   :33.50  
      T15             Ne9             Ne12      
 Min.   :14.90   Min.   :0.000   Min.   :0.000  
 1st Qu.:19.27   1st Qu.:3.000   1st Qu.:4.000  
 Median :22.05   Median :6.000   Median :5.000  
 Mean   :22.63   Mean   :4.929   Mean   :5.018  
 3rd Qu.:25.40   3rd Qu.:7.000   3rd Qu.:7.000  
 Max.   :35.50   Max.   :8.000   Max.   :8.000  
      Ne15           Vx9               Vx12       
 Min.   :0.00   Min.   :-7.8785   Min.   :-7.878  
 1st Qu.:3.00   1st Qu.:-3.2765   1st Qu.:-3.565  
 Median :5.00   Median :-0.8660   Median :-1.879  
 Mean   :4.83   Mean   :-1.2143   Mean   :-1.611  
 3rd Qu.:7.00   3rd Qu.: 0.6946   3rd Qu.: 0.000  
 Max.   :8.00   Max.   : 5.1962   Max.   : 6.578  
      Vx15            maxO3v           vent          
 Min.   :-9.000   Min.   : 42.00   Length:112        
 1st Qu.:-3.939   1st Qu.: 71.00   Class :character  
 Median :-1.550   Median : 82.50   Mode  :character  
 Mean   :-1.691   Mean   : 90.57                     
 3rd Qu.: 0.000   3rd Qu.:106.00                     
 Max.   : 5.000   Max.   :166.00                     
    pluie          
 Length:112        
 Class :character  
 Mode  :character

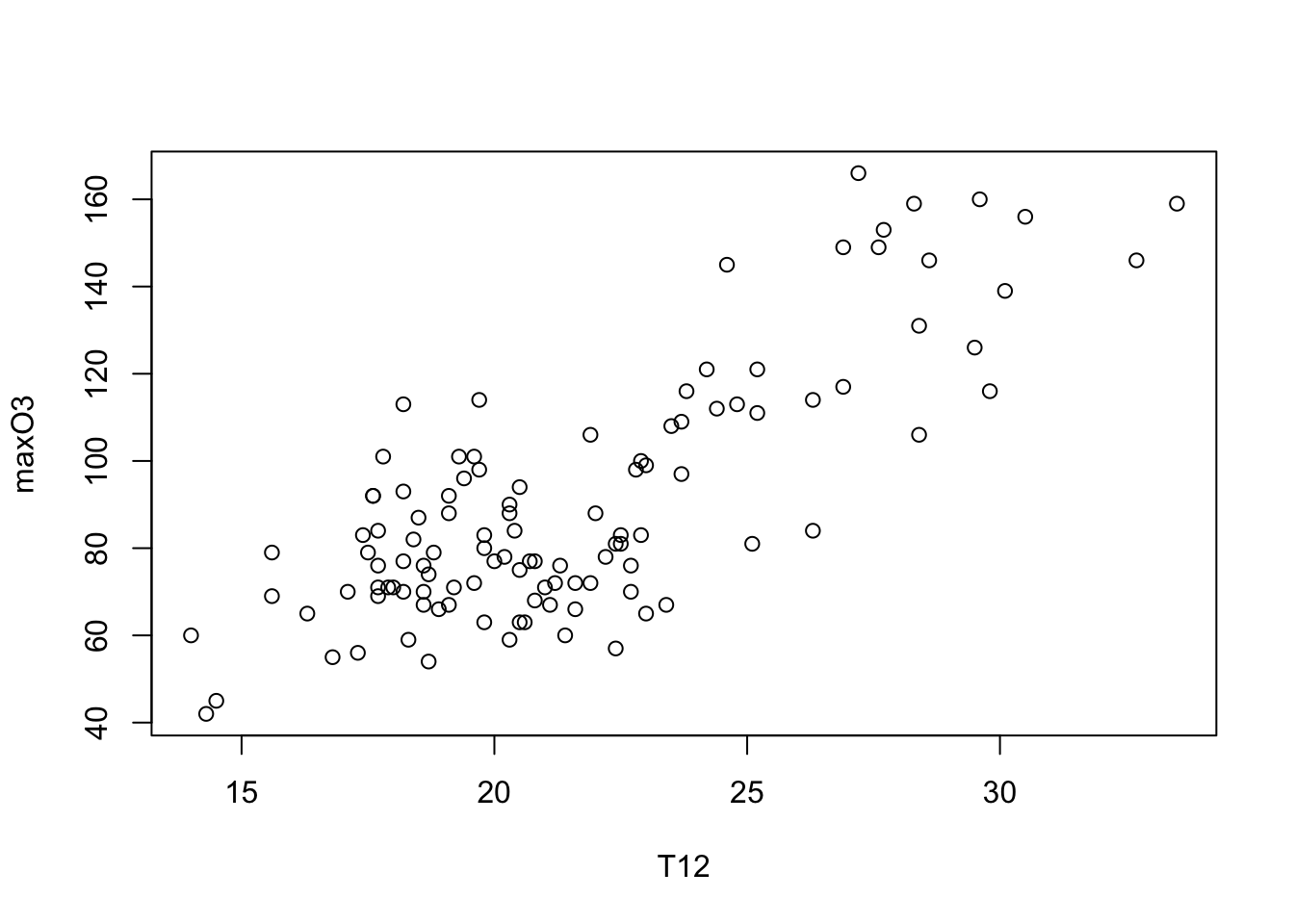
On visualise tout d’abord 2 variables quantitatives à l’aide d’un nuage de points : la concentration en ozone maximale maxO3 en fonction de la température à 12h T12.

plot(ozone[,"T12"],ozone[,"maxO3"])

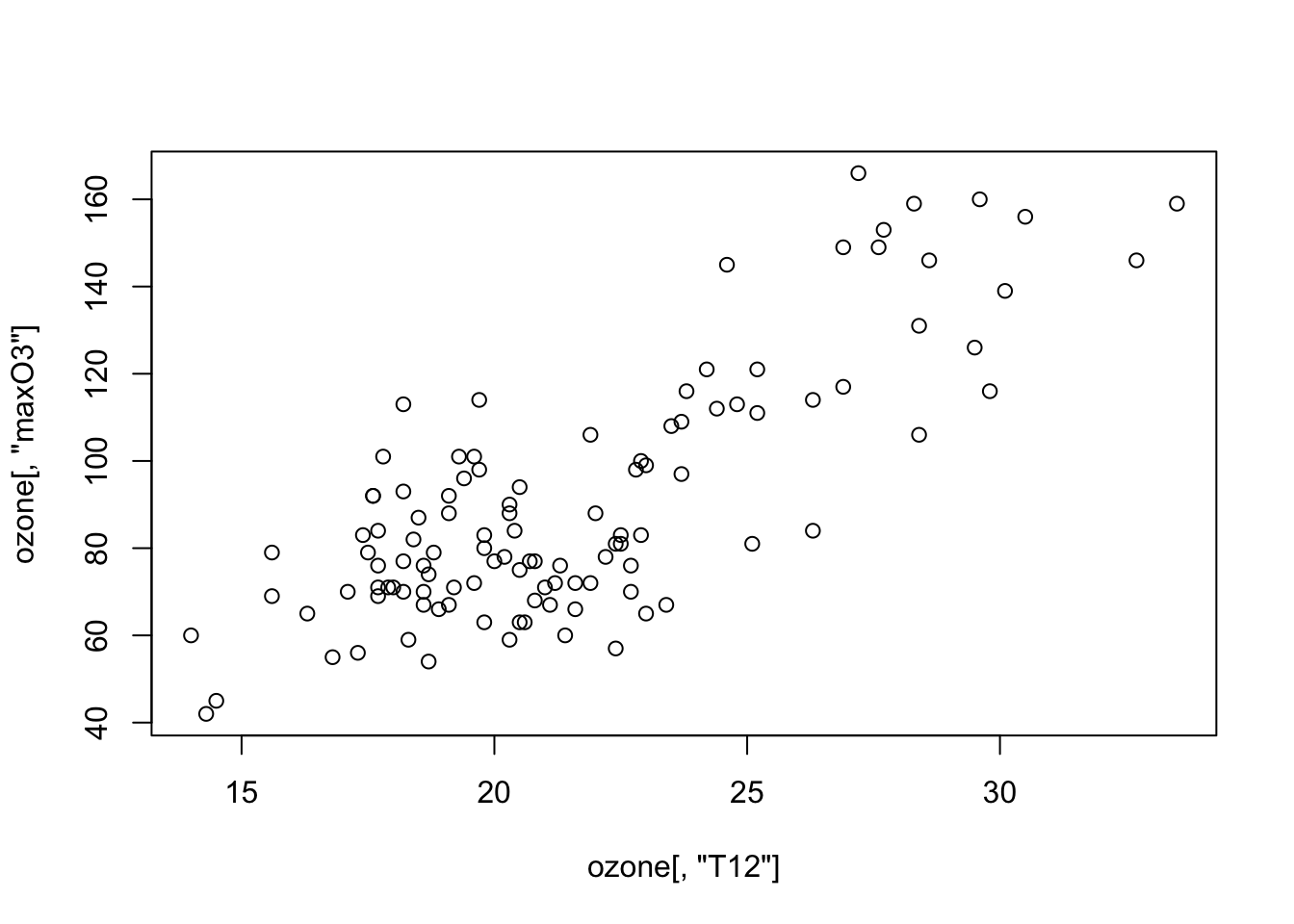
Comme les deux variables appartiennent au même jeu de données, on peut obtenir la même représentation à l’aide d’une sytaxe plus claire qui ajoute automatiquement les noms des variables sur les axes :

plot(maxO3~T12,data=ozone)

Une autre façon de faire (moins naturelle) :

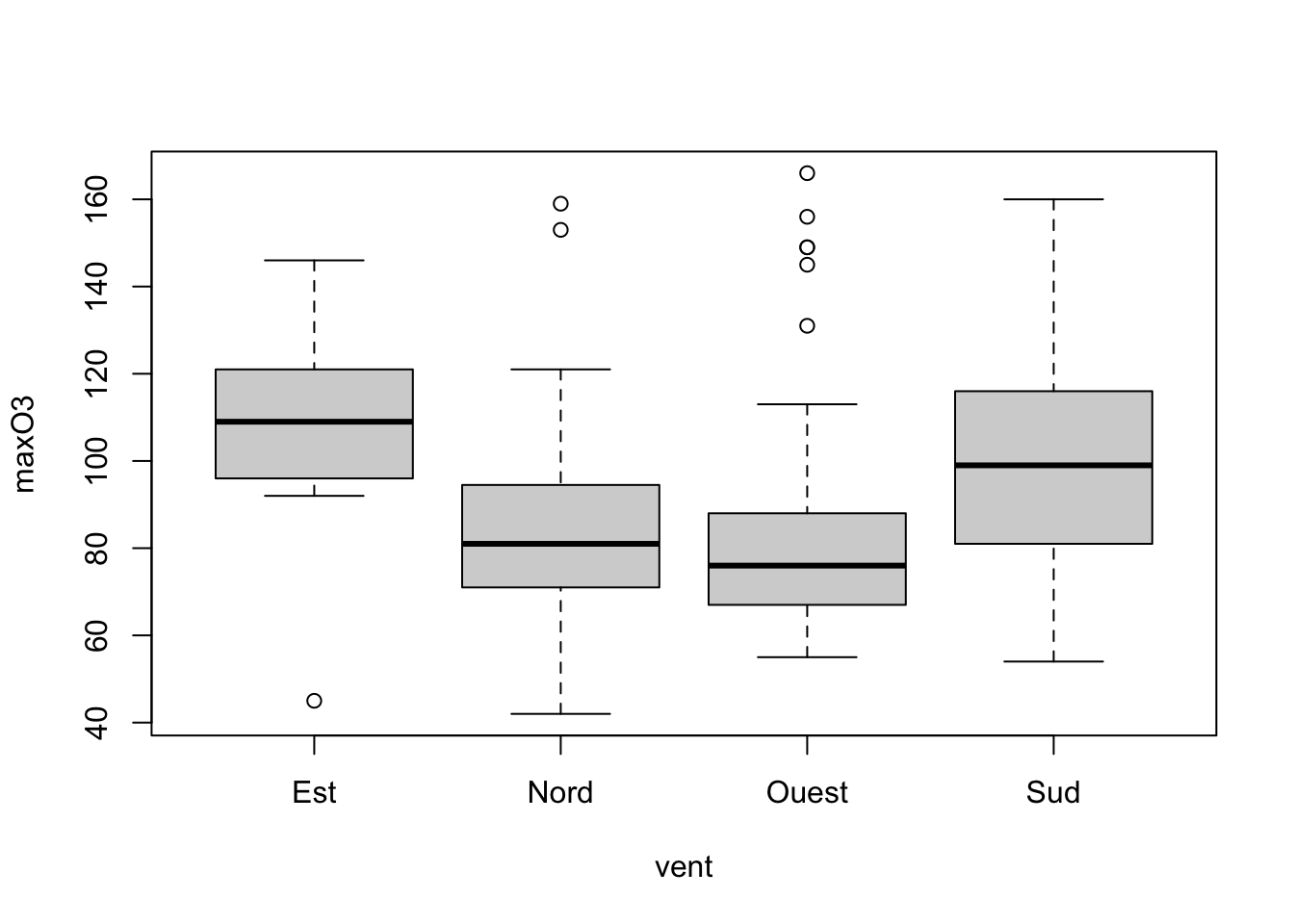
plot(ozone[,"T12"],ozone[,"maxO3"],xlab="T12",ylab="maxO3")

Il existe des fonctions spécifiques pour chaque type de graphes, par exemple histogram, barplot et boxplot :

hist(ozone$maxO3,main="Histogram")

barplot(table(ozone$vent)/nrow(ozone),col="blue")

boxplot(maxO3~vent,data=ozone)

4.1.2 Graphes interactifs avec rAmCharts

On peut utiliser ce package pour obtenir des graphes dynamiques. L’utilisation est relativement simple, il suffit d’ajouter le préfixe am devant le nom de la fonction :

library(rAmCharts)
amHist(ozone$maxO3)

amPlot(ozone,col=c("T9","T12")) amBoxplot(maxO3~vent,data=ozone)

4.1.3 Quelques exercices

Exercice 4.1 (Premier graphe)

Tracer la fonction sinus entre \(0\) et \(2\pi\).
A l’aide de la fonction title ajouter le titre Représentation de la fonction sinus.

Exercice 4.2 (Tracé de densités)

Tracer la densité de la loi normale centrée réduite entre \(-4\) et 4 (utiliser dnorm).
Ajouter une ligne verticale (en tirets) qui passe par \(x=0\) (utiliser abline avec lty=2).
Sur le même graphe, ajouter les densités de loi la de Student à 5 et 30 degrés de liberté (utiliser dt). On utilisera la fonction lines et des couleurs différentes pour chaque densité.
Ajouter une légende qui permet de repérer chaque densité (fonction legend).

Exercice 4.3 (Tâches solaires)

Importer la série taches_solaires.csv qui donne, date par date, un nombre de taches solaires observées.
A l’aide de la fonction cut_interval du tidyverse créer un facteur qui sépare l’intervalle d’années d’observation en 8 intervalles de tailles à peu près égales. On appellera periode ce facteur.

Utiliser les levels suivants pour le facteur periode.

couleurs <- c("yellow", "magenta", "orange", "cyan",
          "grey", "red", "green", "blue")

Expliquer la sortie de la fonction
Visualiser la série du nombre de taches en utilisant une couleur différente pour chaque période.

Exercice 4.4 (Layout)

On reprend le jeu de données sur l’ozone. A l’aide de la fonction layout séparer la fenêtre graphique en deux lignes avec

un graphe sur la première ligne (nuage de points maxO3 vs T12)
2 graphes sur la deuxième ligne (histogramme de T12 et boxplot de maxO3).

4.2 La grammaire ggplot2

Ce package propose de définir des graphes sur R en utilisant une grammaire des graphiques (tout comme dplyr pour manipuler les données). On peut trouver de la documentation sur ce package aux url http://ggplot2.org et https://ggplot2-book.org.

4.2.1 Premiers graphes `ggplot2`

Nous considérons un sous échantillon du jeu de données diamonds du package ggplot2 (qui se trouve dans le tidyverse).

library(tidyverse)
set.seed(1234)
diamonds2 <- diamonds[sample(nrow(diamonds),5000),] 
summary(diamonds2)
     carat               cut       color       clarity    
 Min.   :0.2000   Fair     : 158   D: 640   SI1    :1189  
 1st Qu.:0.4000   Good     : 455   E: 916   VS2    :1157  
 Median :0.7000   Very Good:1094   F: 900   SI2    : 876  
 Mean   :0.7969   Premium  :1280   G:1018   VS1    : 738  
 3rd Qu.:1.0400   Ideal    :2013   H: 775   VVS2   : 470  
 Max.   :4.1300                    I: 481   VVS1   : 326  
                                   J: 270   (Other): 244  
     depth           table           price      
 Min.   :43.00   Min.   :49.00   Min.   :  365  
 1st Qu.:61.10   1st Qu.:56.00   1st Qu.:  945  
 Median :61.80   Median :57.00   Median : 2376  
 Mean   :61.76   Mean   :57.43   Mean   : 3917  
 3rd Qu.:62.50   3rd Qu.:59.00   3rd Qu.: 5294  
 Max.   :71.60   Max.   :95.00   Max.   :18757  
                                                
       x                y               z        
 Min.   : 0.000   Min.   :3.720   Min.   :0.000  
 1st Qu.: 4.720   1st Qu.:4.720   1st Qu.:2.920  
 Median : 5.690   Median :5.700   Median :3.520  
 Mean   : 5.728   Mean   :5.731   Mean   :3.538  
 3rd Qu.: 6.530   3rd Qu.:6.520   3rd Qu.:4.030  
 Max.   :10.000   Max.   :9.850   Max.   :6.430  
                                                 
help(diamonds)

Pour un jeu de données considéré, un graphe ggplot est défini à partir de couches que l’on assemblera avec l’opérateur +. Il faut a minima spécifier :

les données
les variables que l’on souhaite représenter
le type de représentation (nuage de points, boxplot…).

Il existe un verbe pour définir chacune de ces couches :

ggplot pour les données
aes (aesthetics) pour les variables
geom_ pour le type de représentation.

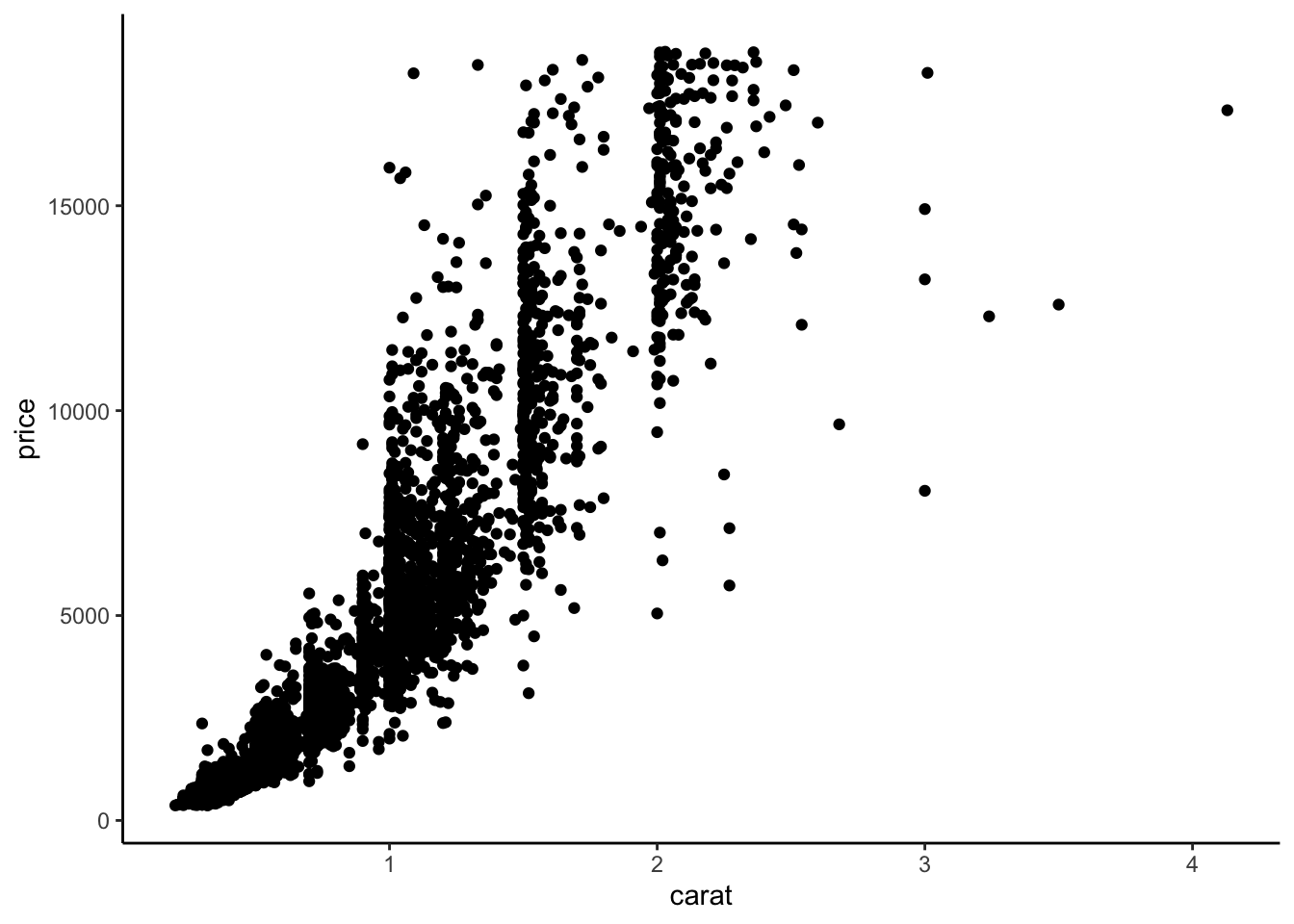
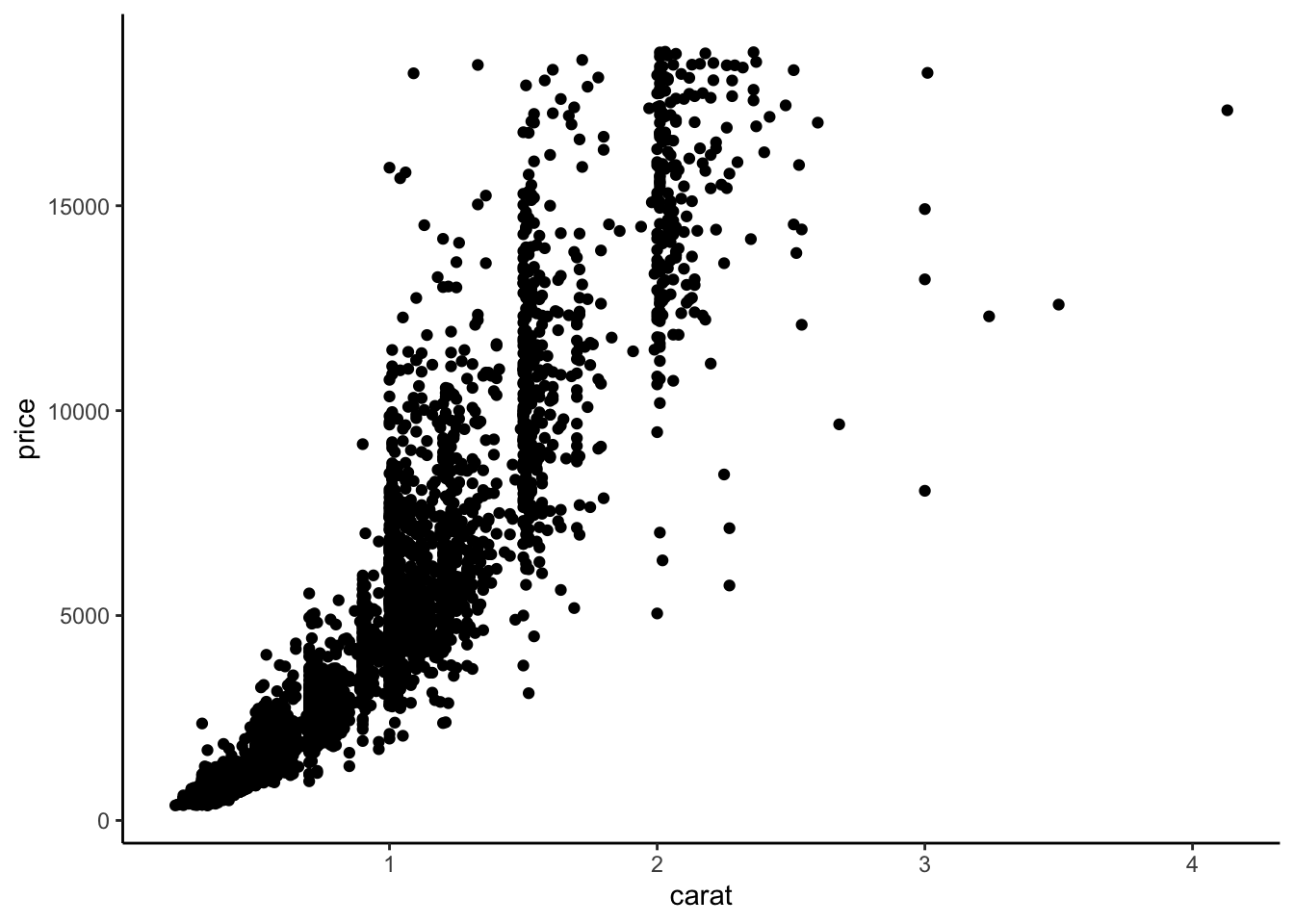
On peut obtenir le nuage de points carat vs price avec la fonction plot :

plot(price~carat,data=diamonds2)

Avec ggplot, on va faire

ggplot(diamonds2) #rien

ggplot(diamonds2)+aes(x=carat,y=price) #rien

ggplot(diamonds2)+aes(x=carat,y=price)+geom_point() #bon

Exercice 4.5 (Premiers graphes ggplot)

Tracer l’histogramme de la variable carat (utiliser geom_histogram).
Tracer l’histogramme de la variable carat avec 10 classes (help(geom_histogram)).
Tracer le diagramme en barres de la variable cut (utiliser geom_bar).

La syntaxe ggplot se construit à partir d’éléments indépendants qui définissent la grammaire de ggplot. Les principaux verbes sont :

Data (ggplot) : les données au format dataframe ou tibble
Aesthetics (aes) : pour sépecifier les variables à représenter dans le graphe.
Geometrics (geom_...) : le type de graphe (nuage de points, histogramme…).
Statistics (stat_...) : utile pour spécifier des transformations des données nécessaires pour obtenir le graphe.
Scales (scale_...) : pour controler les paramètres permettant d’affiner le graphe (changement de couleurs, paramètres des axes…).

Tous ces éléments sont reliés avec le symbole +.

4.2.2 Data et aesthetics

Ces deux verbes sont à utiliser pour tous les graphes ggplot. Le verbe ggplot servira à définir le jeu de données que l’on souhaite utiliser. Si le code est bien fait, nous n’aurons plus à utiliser le nom du jeu de données par la suite pour construire le graphe. Le verbe aes est quant à lui utile pour spécifier le nom des variables que l’on souhaite visualiser. Par exemple, pour le nuage de points price vs carat la syntaxe devra débuter par

ggplot(diamonds2)+aes(x=carat,y=price)

Les variables peuvent également être utilisées pour colorier des points ou des barres, définir des tailles… Dans ce cas on pourra renseigner les arguments color, size, fill dans la fonction aes. Par exemple

ggplot(diamonds2)+aes(x=carat,y=price,color=cut)

4.2.3 Geometrics

Ce verbe décrira le type de représentation souhaité. Pour un nuage de points, on utilisera par exemple geom_point :

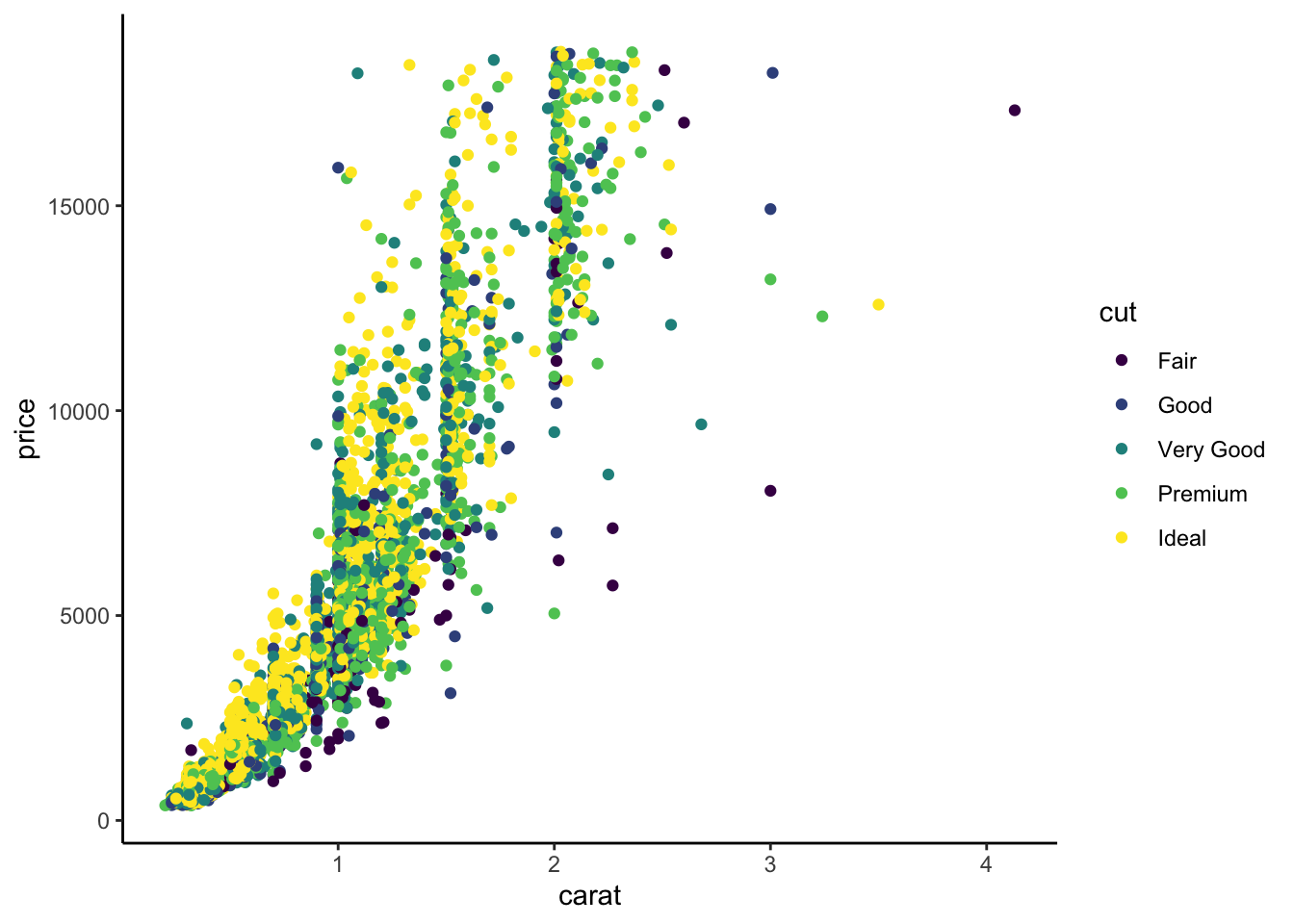
ggplot(diamonds2)+aes(x=carat,y=price,color=cut)+geom_point()

On observe que ggplot ajoute la légende automatiquement. Voici les principaux exemples de geometrics :

Table 4.1: Principaux geometrics
Geom	Description	Aesthetics
geom_point()	nuage de points	x, y, shape, fill
geom_line()	Ligne (ordonnée selon x)	x, y, linetype
geom_abline()	Ligne	slope, intercept
geom_path()	Ligne (ordonnée par l’index)	x, y, linetype
geom_text()	Texte	x, y, label, hjust, vjust
geom_rect()	Rectangle	xmin, xmax, ymin, ymax, fill, linetype
geom_polygon()	Polygone	x, y, fill, linetype
geom_segment()	Segment	x, y, xend, yend, fill, linetype
geom_bar()	Diagramme en barres	x, fill, linetype, weight
geom_histogram()	Histogramme	x, fill, linetype, weight
geom_boxplot()	Boxplot	x, fill, weight
geom_density()	Densité	x, y, fill, linetype
geom_contour()	Lignes de contour	x, y, fill, linetype
geom_smooth()	Lisseur (linéaire ou non linéaire)	x, y, fill, linetype
Tous		color, size, group

Exercice 4.6 (Diagrammes en barres)

Tracer le diagramme en barres de la variable cut avec des barres bleues.
Tracer le diagramme en barres de la variable cut avec une couleur pour chaque modalité de cut ainsi qu’une légende qui permet de repérer la couleur.
Tracer le diagramme en barres de la variable cut avec une couleur pour chaque modalité que vous choisirez (et sans légende).

4.2.4 Statistics

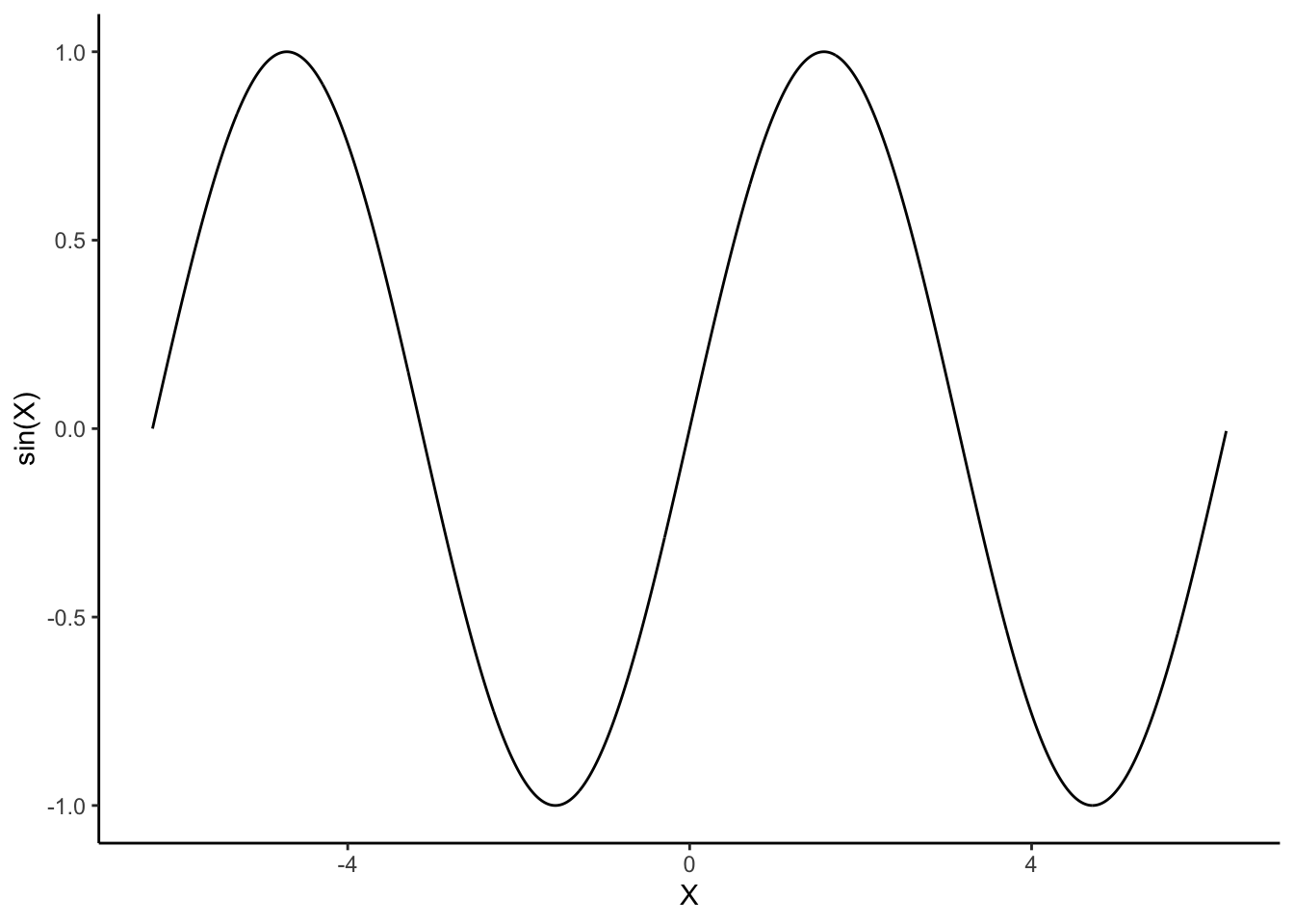
Certains graphes nécessitent des calculs d’indicateurs statistiques pour être tracé. C’est par exemple le cas pour le diagramme en barres et l’histogramme où il faut calculer des hauteurs de rectangles ou barres. Les transformations simples peuvent se faire rapidement, on peut par exemple tracer la fonction sinus avec

D <- data.frame(X=seq(-2*pi,2*pi,by=0.01))
ggplot(D)+aes(x=X,y=sin(X))+geom_line()

La transformation est spécifiée dans la fonction aes. Pour des transformations plus complexes, nous devons utiliser des statistics. Une fonction stat permet de définir des nouvelles variables à partir du jeu de données initial, il est ensuite possible de représenter ces nouvelles variables. Par exemple, la fonction stat_bin, qui est utilisée par défaut pour construire des histogrammes, produit les variables suivantes :

count, le nombre d’observations dans chaque classes.
density, la valeur de la densité des observations dans chaque classe (fréquance divisée par largeur de la classe).
x, le centre de la classe.

Par défaut geom_histogram fait appel à cette fonction stat_binet représente sur l’axe \(y\) le nombre d’observations dans chaque classe (la variable count).

ggplot(diamonds2)+aes(x=price)+geom_histogram(bins=40)

Si on souhaite une autre variable issue de stat_bin, comme par exemple la densité, il faudra utiliser

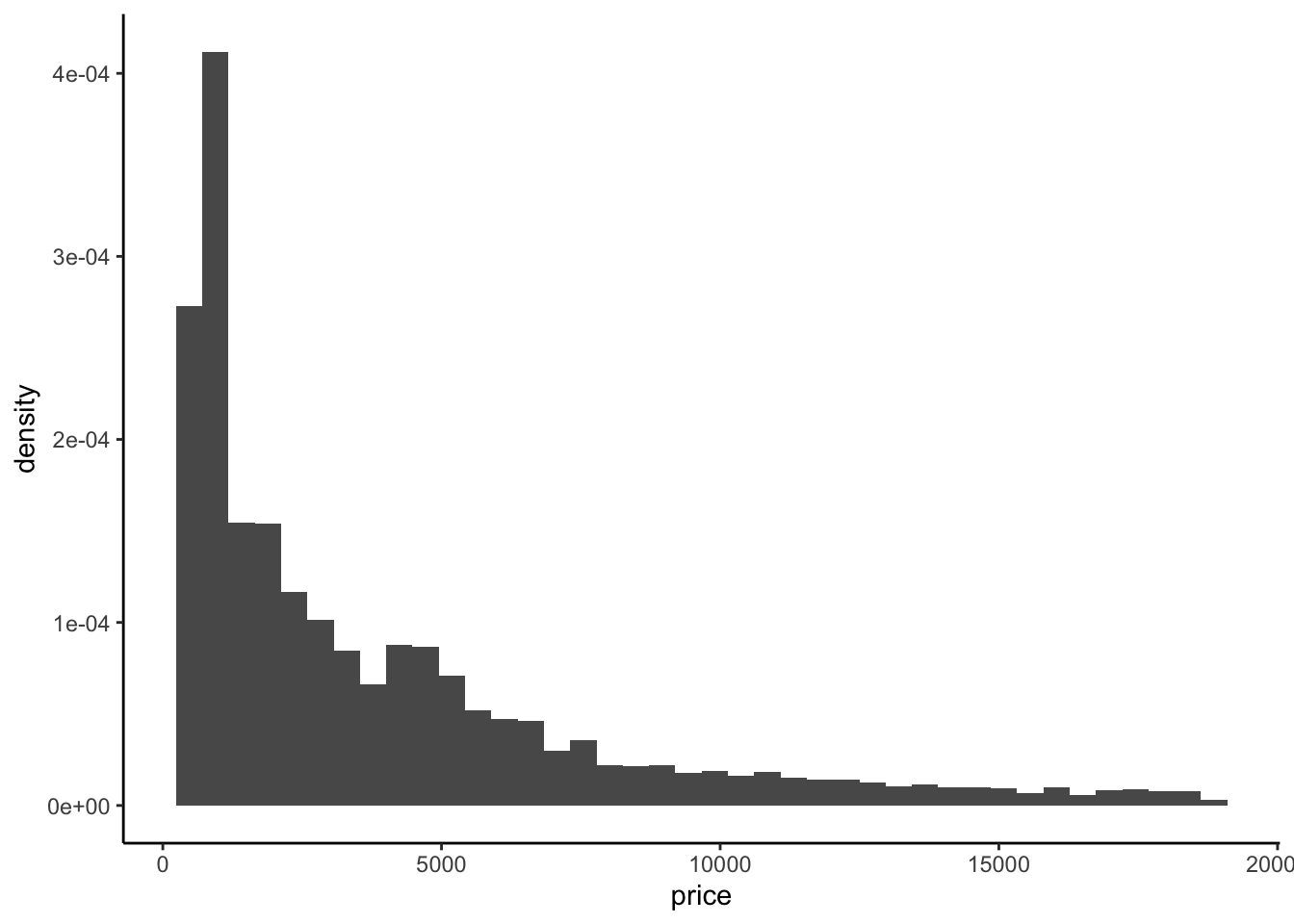
ggplot(diamonds2)+aes(x=price,y=..density..)+geom_histogram(bins=40)

Il est possible d’utiliser les fonctions stat_ à la place des geom_ pour certaines représentations. Chaque fonction stat_ possède par défaut un geom_ et réciproquement. On peut par exemple obtenir le même graphe que précédemment avec

ggplot(diamonds2)+aes(x=price,y=..density..)+stat_bin()

Voici quelques exemple de fonctions stat_

Table 4.2: Exemples de statistics.
Stat	Description	Paramètres
stat_identity()	aucune transformation
stat_bin()	Count	binwidth, origin
stat_density()	Density	adjust, kernel
stat_smooth()	Smoother	method, se
stat_boxplot()	Boxplot	coef

stat et geom ne sont pas toujours simples à combiner. Nous recommandons d’utiliser geom lorsqu’on débute avec ggplot, les statisticspar défaut ne doivent en effet être changés que rarement.

Exercice 4.7 (Diagramme en barres “très simple”…)

On considère une variable qualitative \(X\) dont la loi est donnée par \[P(X=\text{red})=0.3,\ P(X=\text{blue})=0.2,\ P(X=\text{green})=0.4,\ P(X=\text{black})=0.1\] Représenter cette distribution de probabilité avec un diagramme en barres.

Exercice 4.8 (Lissage)

Représenter le lissage non linéaire de la variable price contre la variable carat à l’aide de geom_smooth puis de stat_smooth.
Même question mais avec une ligne en pointillés à la place d’un trait plein.

4.2.5 Scales

Les échelles (scales) controlent tout un tas d’options telles que des changements de couleurs, d’échelles ou de limites d’axes, de symboles, etc… L’utilisation n’est pas simple et nécessite de la pratique. On utilise généralement ce verbe à la dernière étape de construction du graphe. La syntaxe est définie comme suit :

début : scale_.
ajout de l’aesthetics que l’on souhaite modifier (color_, fill_, x_).
fin : nom de l’échelle (manual, identity…)

Par exemple,

ggplot(diamonds2)+aes(x=carat,y=price,color=cut)+geom_point()+
  scale_color_manual(values=c("Fair"="black","Good"="yellow",
                              "Very Good"="blue","Premium"="red","Ideal"="green"))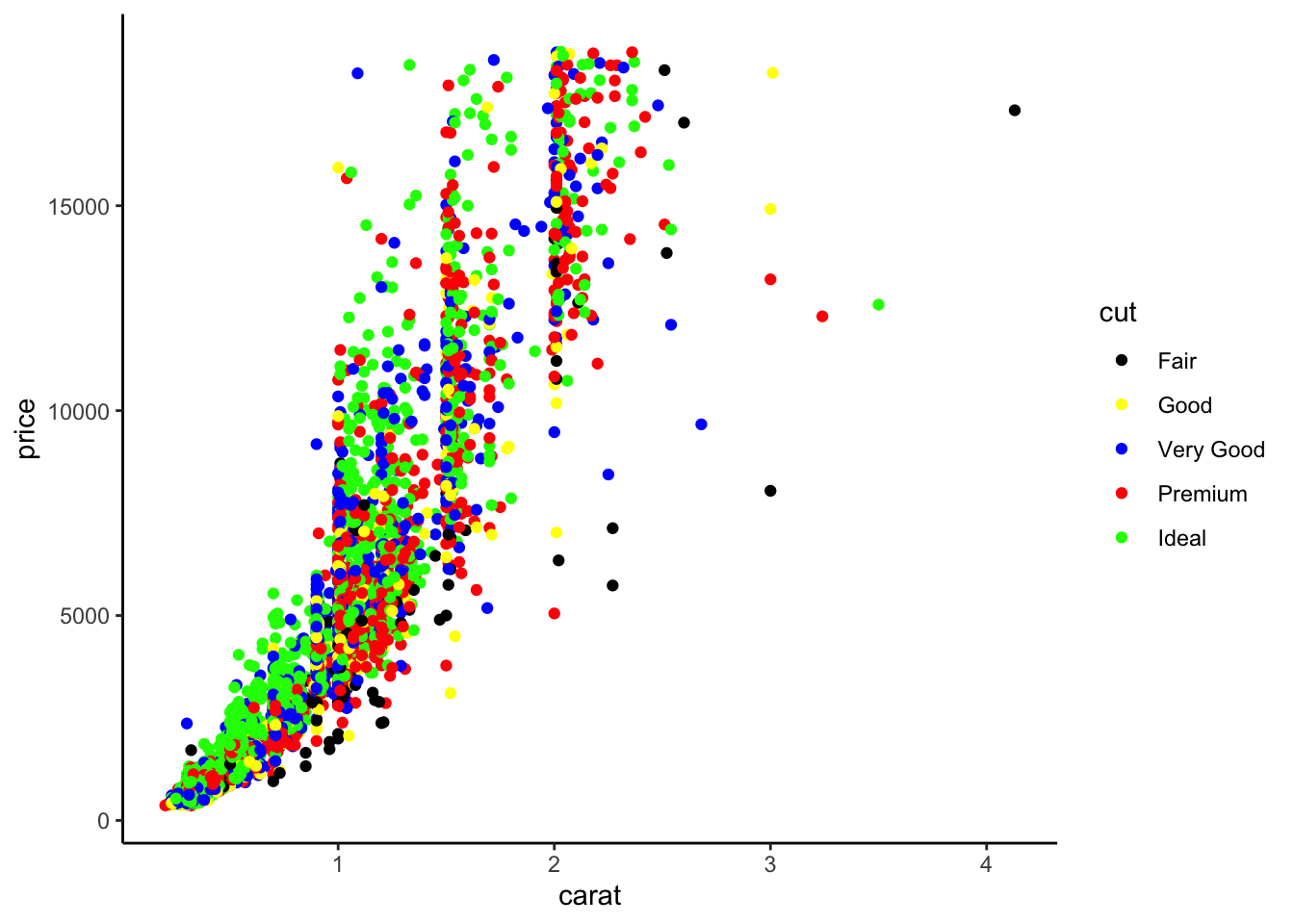

Voici quelques exemples des principales échelles :

Table 4.3: Exemples d’échelles
aes	Discret	Continu
Couleur (color et fill)	brewer	gradient
-	grey	gradient2
-	hue	gradientn
-	identity
-	manual
Position (x et y)	discrete	continous
-		date
Forme	shape
-	identity
-	manual
Taille	identity	size
-	manual

Nous présentons quelques exemples d’utilisation des échelles :

Couleur dans un diagramme en barres

p1 <- ggplot(diamonds2)+aes(x=cut)+geom_bar(aes(fill=cut))
p1

On change la couleur en utilisant la palette Purples :

p1+scale_fill_brewer(palette="Purples")

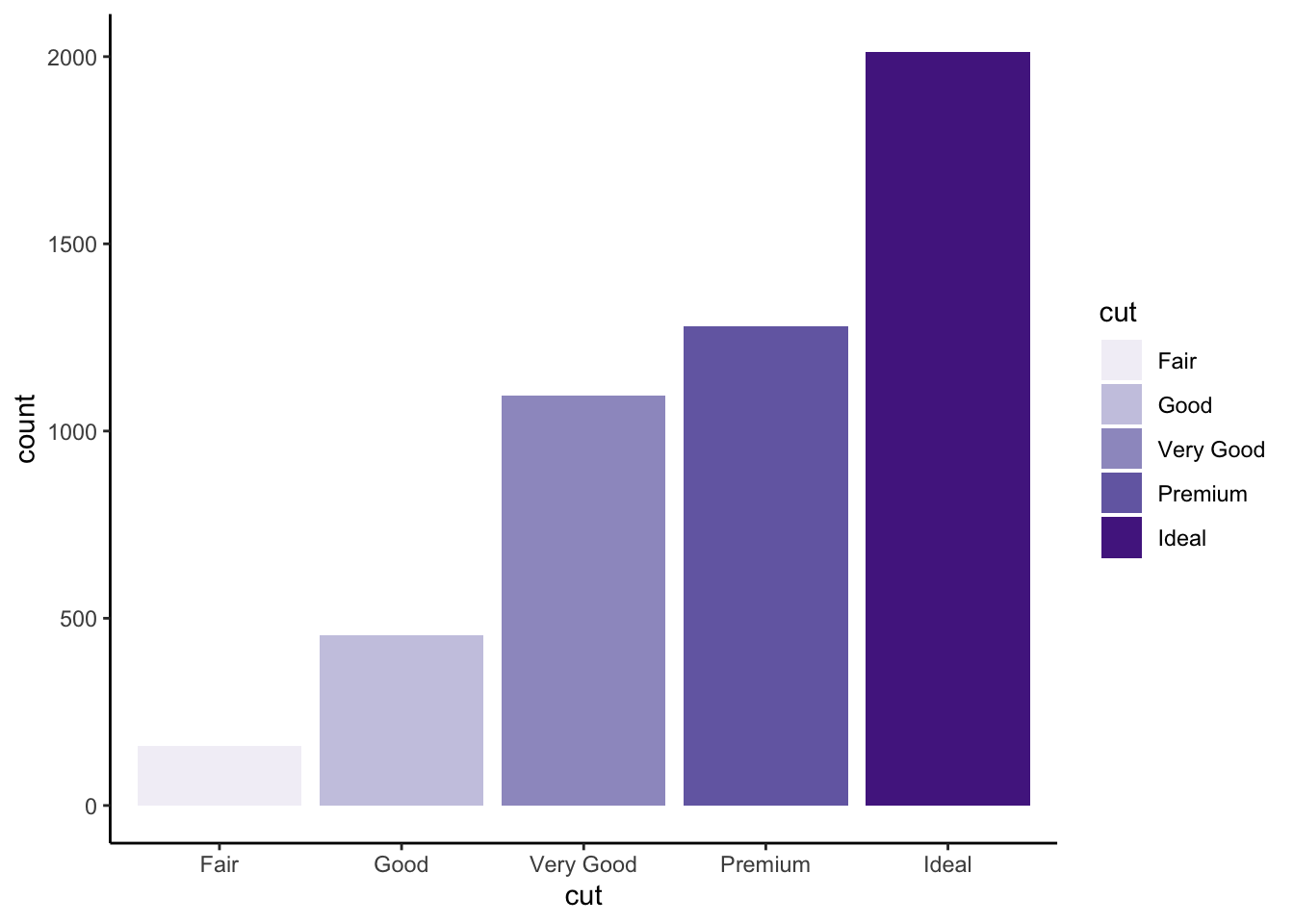
Gradient de couleurs pour un nuage de points :

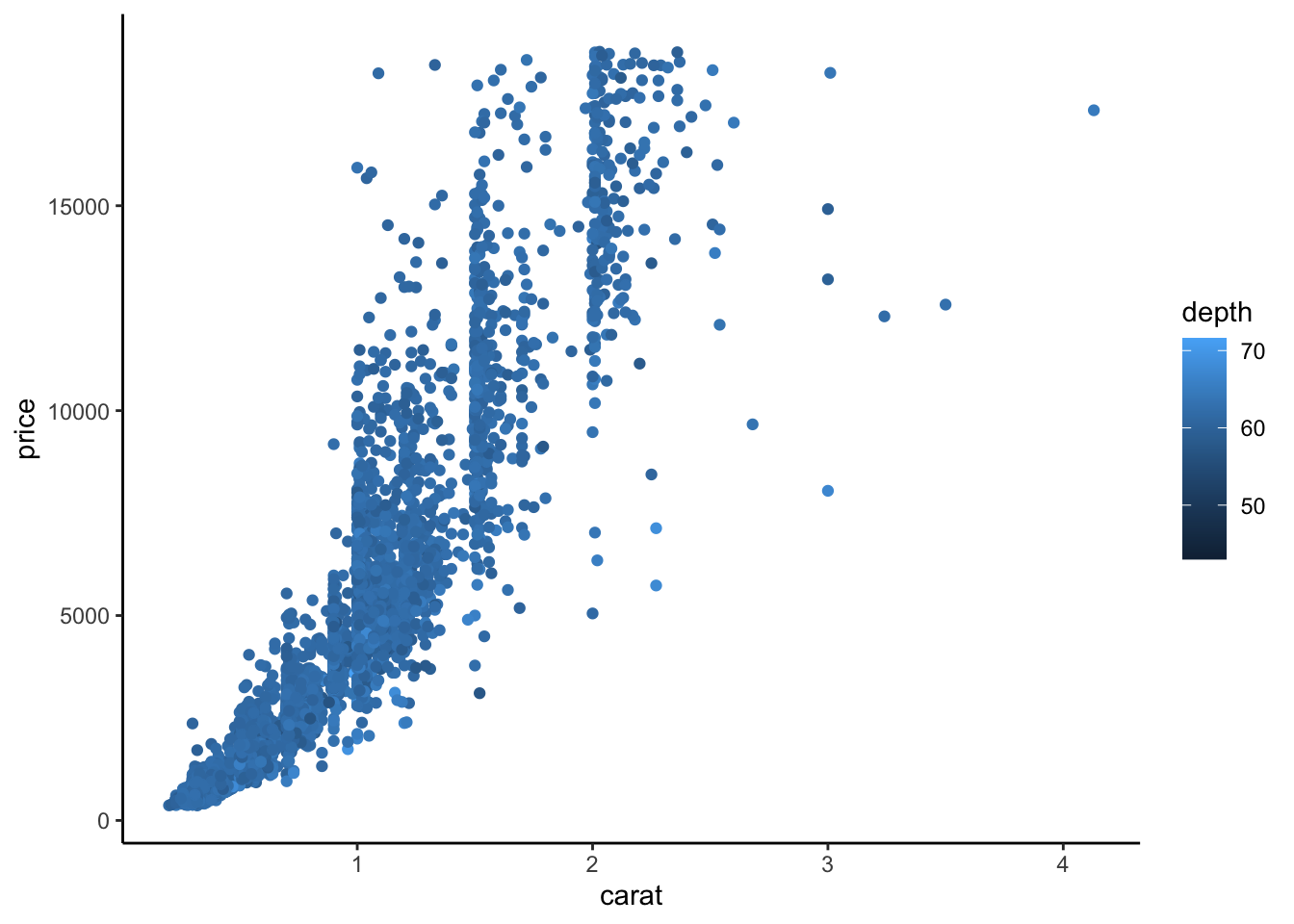p2 <- ggplot(diamonds2)+aes(x=carat,y=price)+geom_point(aes(color=depth))
p2

On change le gradient de couleur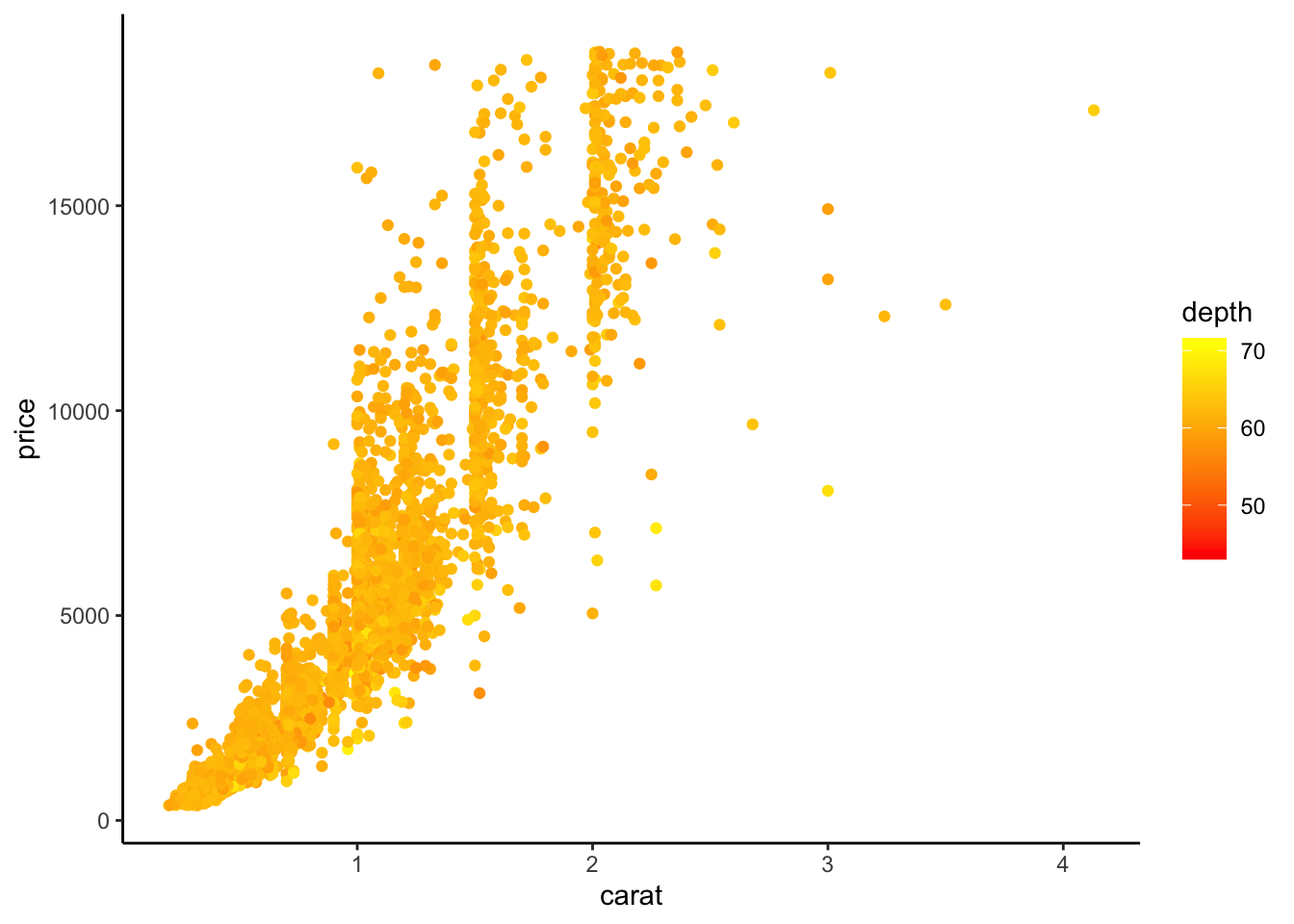

p2+scale_color_gradient(low="red",high="yellow")

Modifications sur les axes

p2+scale_x_continuous(breaks=seq(0.5,3,by=0.5))+
  scale_y_continuous(name="prix")+
  scale_color_gradient("Profondeur")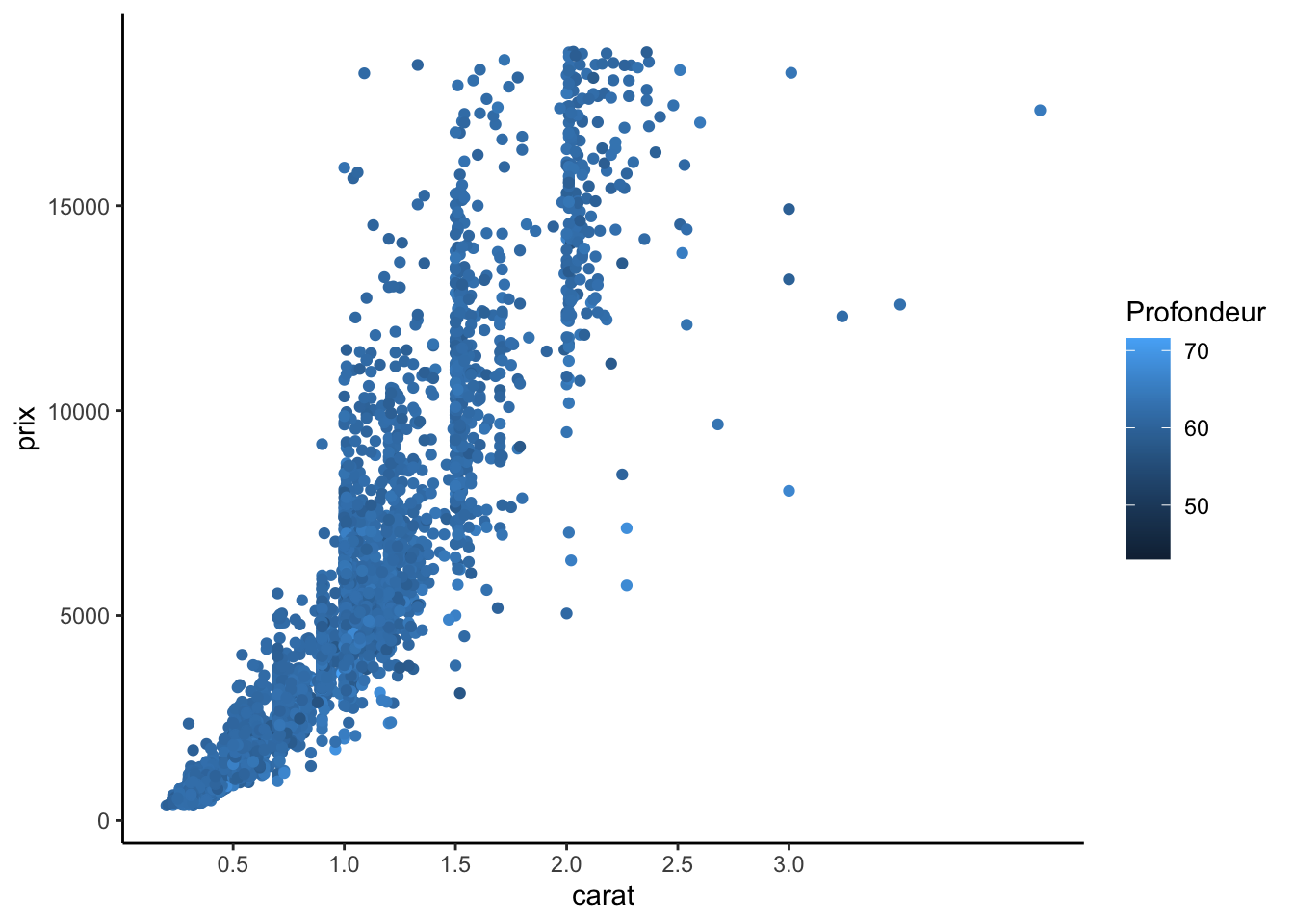

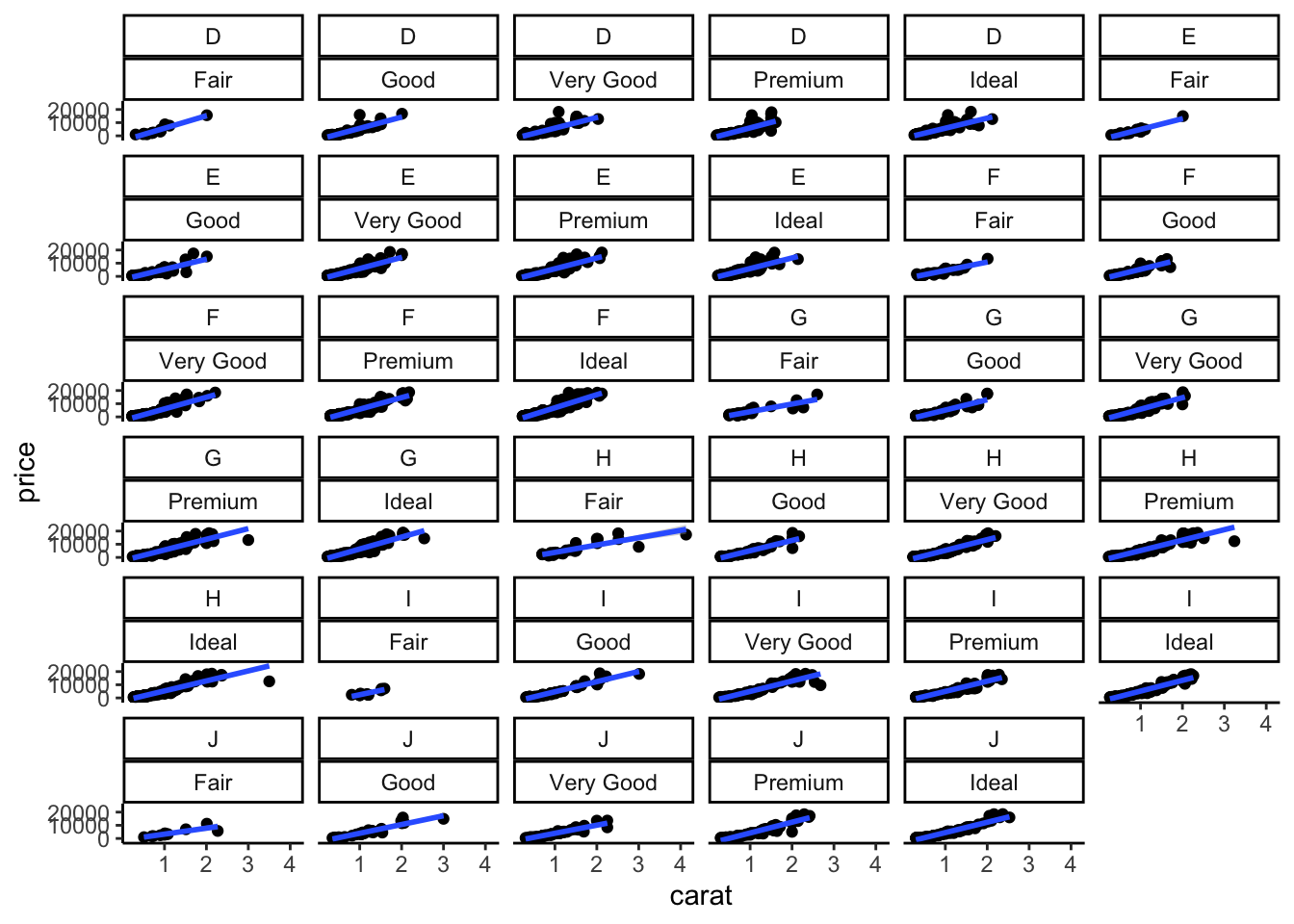
4.2.6 Group et facets

ggplot permet de faire des représentations pour des groupes d’individus. On procède généralement de deux façons différentes :

visualisation de sous groupes sur le même graphe, on utilise l’option group dans le verbe aes ;
visualisation de sous groupes sur des graphes différents, on utilise le verbe facet_wrap ou facet_grid.

Représentons ici (sur le même graphe) le lisseur price vs carat pour chaque modalité de cut

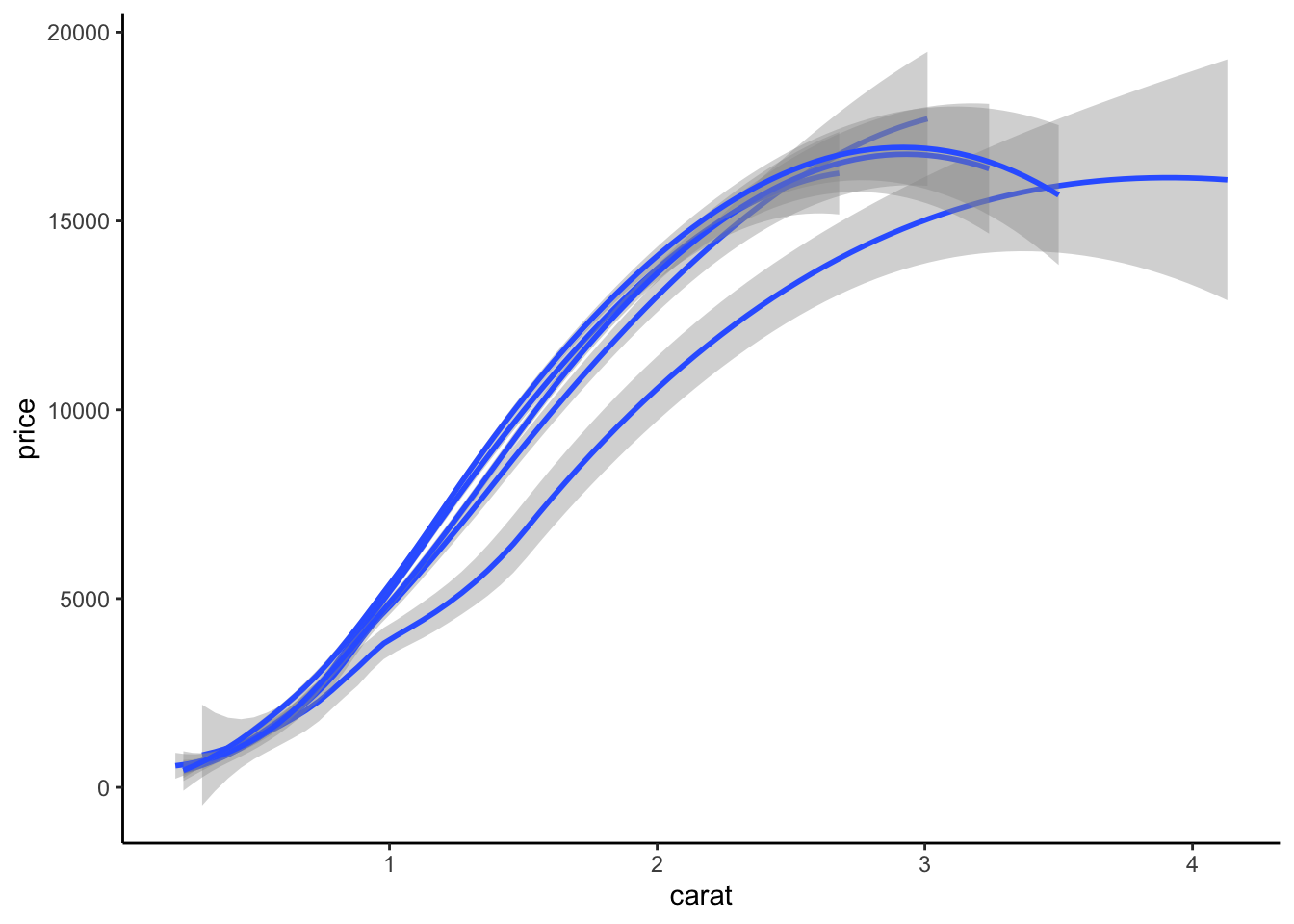
ggplot(diamonds2)+aes(x=carat,y=price,group=cut)+
  geom_smooth(method="loess")

Pour obtenir cette représentation sur plusieurs fenêtres, on utilise

ggplot(diamonds2)+aes(x=carat,y=price)+
  geom_smooth(method="loess")+facet_wrap(~cut)

ggplot(diamonds2)+aes(x=carat,y=price)+
  geom_smooth(method="loess")+facet_wrap(~cut,nrow=1)

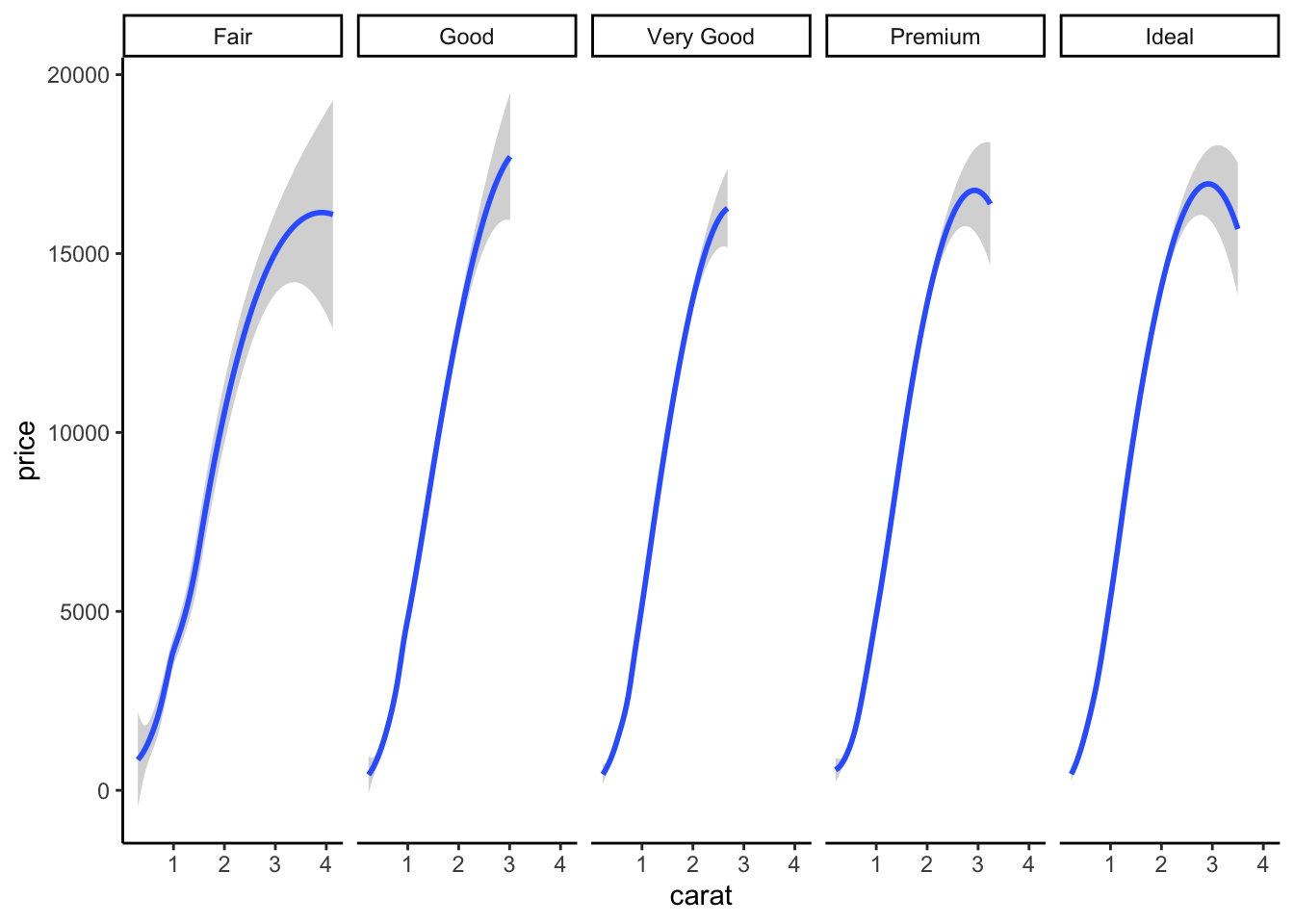
facet_grid et facet_wrap font des choses proches mais divisent la fenêtre d’une façon différente :

ggplot(diamonds2)+aes(x=carat,y=price)+geom_point()+
  geom_smooth(method="lm")+facet_grid(color~cut)

ggplot(diamonds2)+aes(x=carat,y=price)+geom_point()+
  geom_smooth(method="lm")+facet_wrap(color~cut)

4.3 Compléments

La syntaxe ggplot est définie selon le schéma :

ggplot()+aes()+geom_()+scale_()

Elle est très flexible, on peut par exemple spécifier les variables de aes dans les verbes ggplot ou geom_ :

ggplot(diamonds2)+aes(x=carat,y=price)+geom_point()

ggplot(diamonds2,aes(x=carat,y=price))+geom_point()

ggplot(diamonds2)+geom_point(aes(x=carat,y=price))

Ceci peut se révéler très utile lorsqu’on utilise des aes différents dans les geom_.

On peut aussi construire un graphe à l’aide de différents jeux de données :

X <- seq(-2*pi,2*pi,by=0.001)
Y1 <- cos(X)
Y2 <- sin(X)
donnees1 <- data.frame(X,Y1)
donnees2 <- data.frame(X,Y2)
ggplot(donnees1)+geom_line(aes(x=X,y=Y1))+
  geom_line(data=donnees2,aes(x=X,y=Y2),color="red")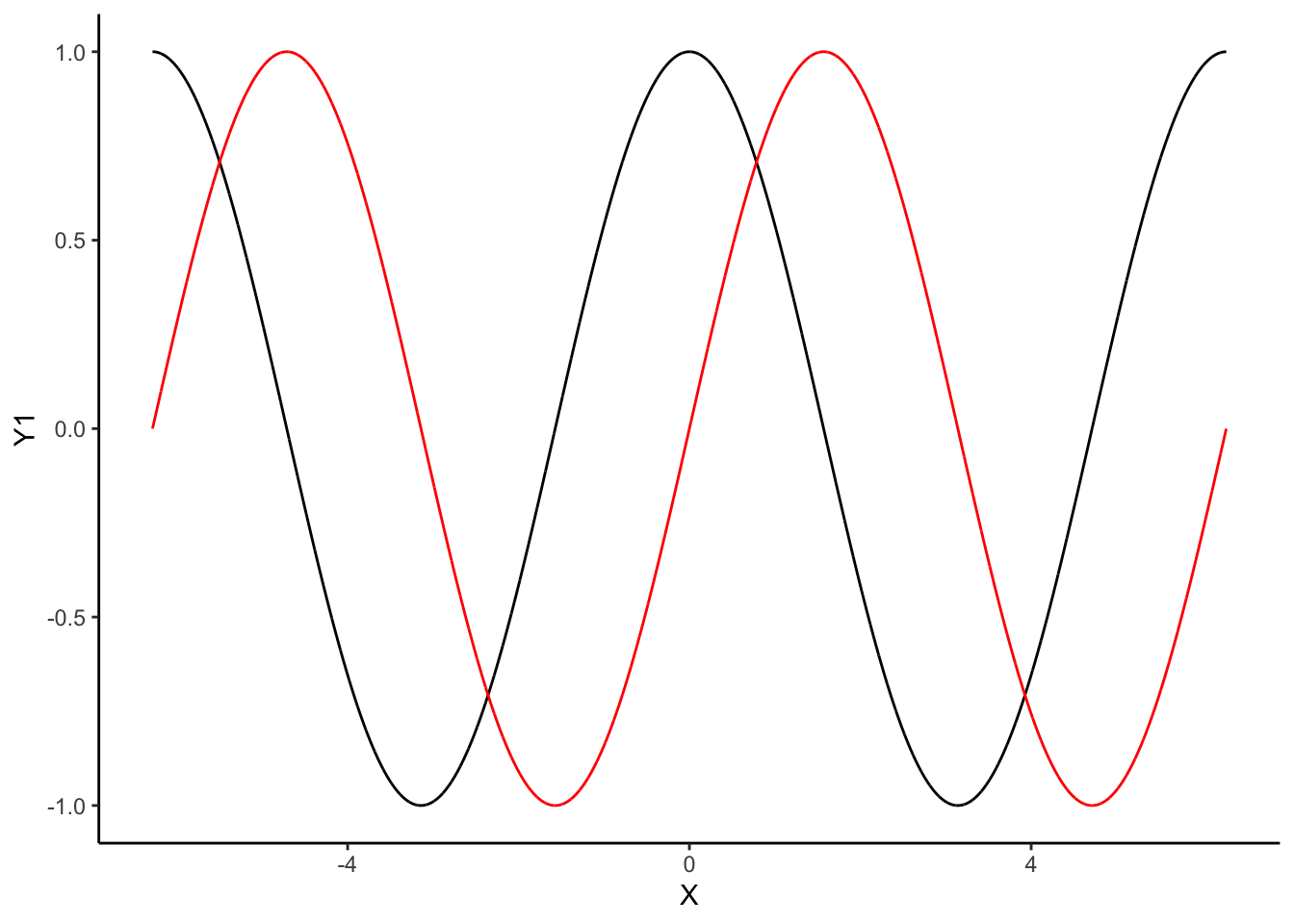

Il existe d’autres fonctions ggplot :

ggtitle pour ajouter un titre.
ggsave pour sauver un graphe.
theme_ pour changer le theme du graphe.

p <- ggplot(diamonds2)+aes(x=carat,y=price,color=cut)+geom_point()
p+theme_bw()

p+theme_classic()

p+theme_grey()

p+theme_bw()

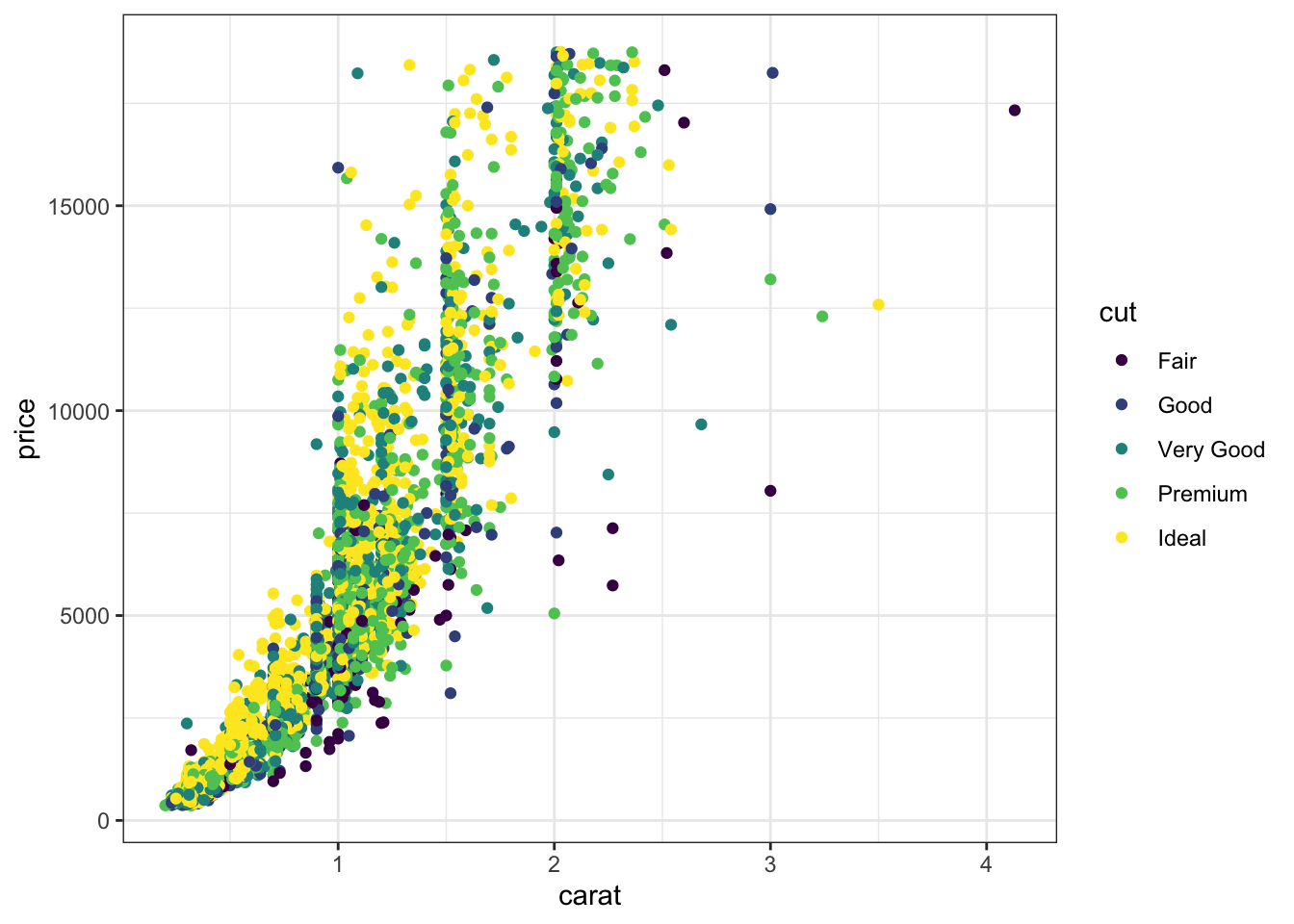
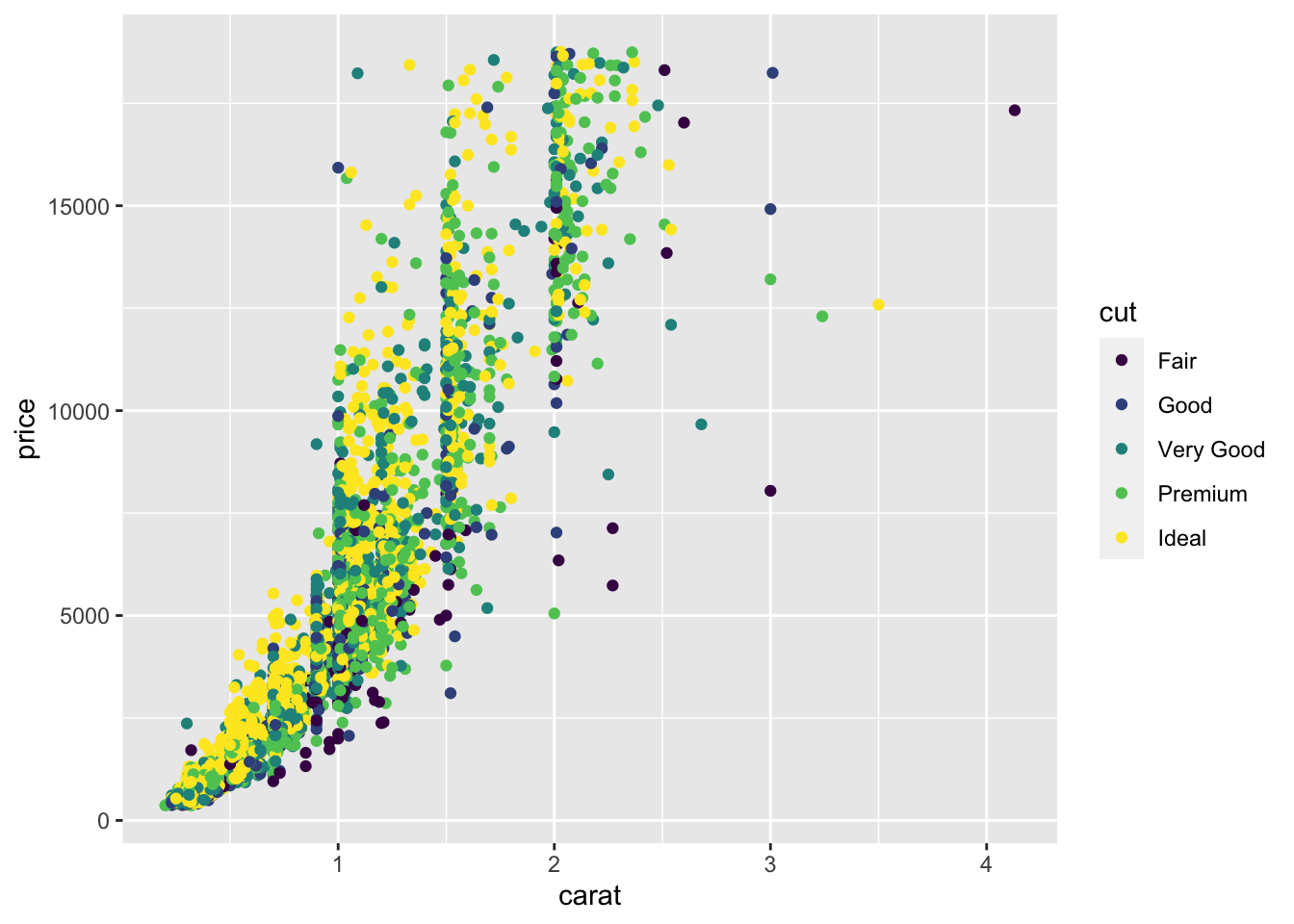
D’autres thèmes sont disponibles dans le package ggtheme. On pourra également parler de la fonction set_theme qui permet de modifier le thème par défaut pour un document Markdown.

4.4 Quelques exercices supplémentaires

Exercice 4.9 (Fonctions cosinus et sinus)

Tracer les fonctions sinus et cosinus. On utilisera tout d’abord deux jeux de données : un pour le sinus, l’autre pour le cosinus.
Faire la même chose avec un jeu de données et deux appels à la fonction geom_line. On pourra ajouter une légende.
Faire la même chose avec un jeu de données et un seul appel à geom_line. On pourra utiliser la fonction pivot_longer du tidyverse.
Tracer les deux fonctions sur deux fenêtres graphiques (utiliser facet_wrap).
Faire la même chose avec la fonction grid.arrange du package gridExtra.

Exercice 4.10 (Différents graphes)

On considère les données mtcars

data(mtcars)
summary(mtcars)
      mpg             cyl             disp      
 Min.   :10.40   Min.   :4.000   Min.   : 71.1  
 1st Qu.:15.43   1st Qu.:4.000   1st Qu.:120.8  
 Median :19.20   Median :6.000   Median :196.3  
 Mean   :20.09   Mean   :6.188   Mean   :230.7  
 3rd Qu.:22.80   3rd Qu.:8.000   3rd Qu.:326.0  
 Max.   :33.90   Max.   :8.000   Max.   :472.0  
       hp             drat             wt       
 Min.   : 52.0   Min.   :2.760   Min.   :1.513  
 1st Qu.: 96.5   1st Qu.:3.080   1st Qu.:2.581  
 Median :123.0   Median :3.695   Median :3.325  
 Mean   :146.7   Mean   :3.597   Mean   :3.217  
 3rd Qu.:180.0   3rd Qu.:3.920   3rd Qu.:3.610  
 Max.   :335.0   Max.   :4.930   Max.   :5.424  
      qsec             vs               am        
 Min.   :14.50   Min.   :0.0000   Min.   :0.0000  
 1st Qu.:16.89   1st Qu.:0.0000   1st Qu.:0.0000  
 Median :17.71   Median :0.0000   Median :0.0000  
 Mean   :17.85   Mean   :0.4375   Mean   :0.4062  
 3rd Qu.:18.90   3rd Qu.:1.0000   3rd Qu.:1.0000  
 Max.   :22.90   Max.   :1.0000   Max.   :1.0000  
      gear            carb      
 Min.   :3.000   Min.   :1.000  
 1st Qu.:3.000   1st Qu.:2.000  
 Median :4.000   Median :2.000  
 Mean   :3.688   Mean   :2.812  
 3rd Qu.:4.000   3rd Qu.:4.000  
 Max.   :5.000   Max.   :8.000

Tracer l’histogramme de mpg (on fera varier le nombre de classes).
Tracer l’histogramme de la densité.
Tracer le diagramme en barres de cyl.
Tracer le nuage de points disp vs mpg en utilisant une couleur différente pour chaque valeur de cyl.
Ajouter le lisseur linéaire sur le graphe (un lisseur par modalité de cyl).

Exercice 4.11 (Résidus pour régression simple)

Générer un échantillon \((x_i,y_i),i=1,\dots,100\) selon le modèle linéaire \[y_i=3+x_i+\varepsilon_i\] où les \(x_i\) sont i.i.d. de loi uniforme sur \([0,1]\) et les \(\varepsilon_i\) sont i.i.d. de loi gaussienne \(N(0,0.2^2)\) (utiliser runif et rnorm).
Tracer le nuage de points Y vs X et ajouter le lisseur linéaire.
Représenter les résidus : on ajoutera une ligne verticale entre chaque point et la droite de lissage (utiliser geom_segment).

Exercice 4.12 (Challenge)

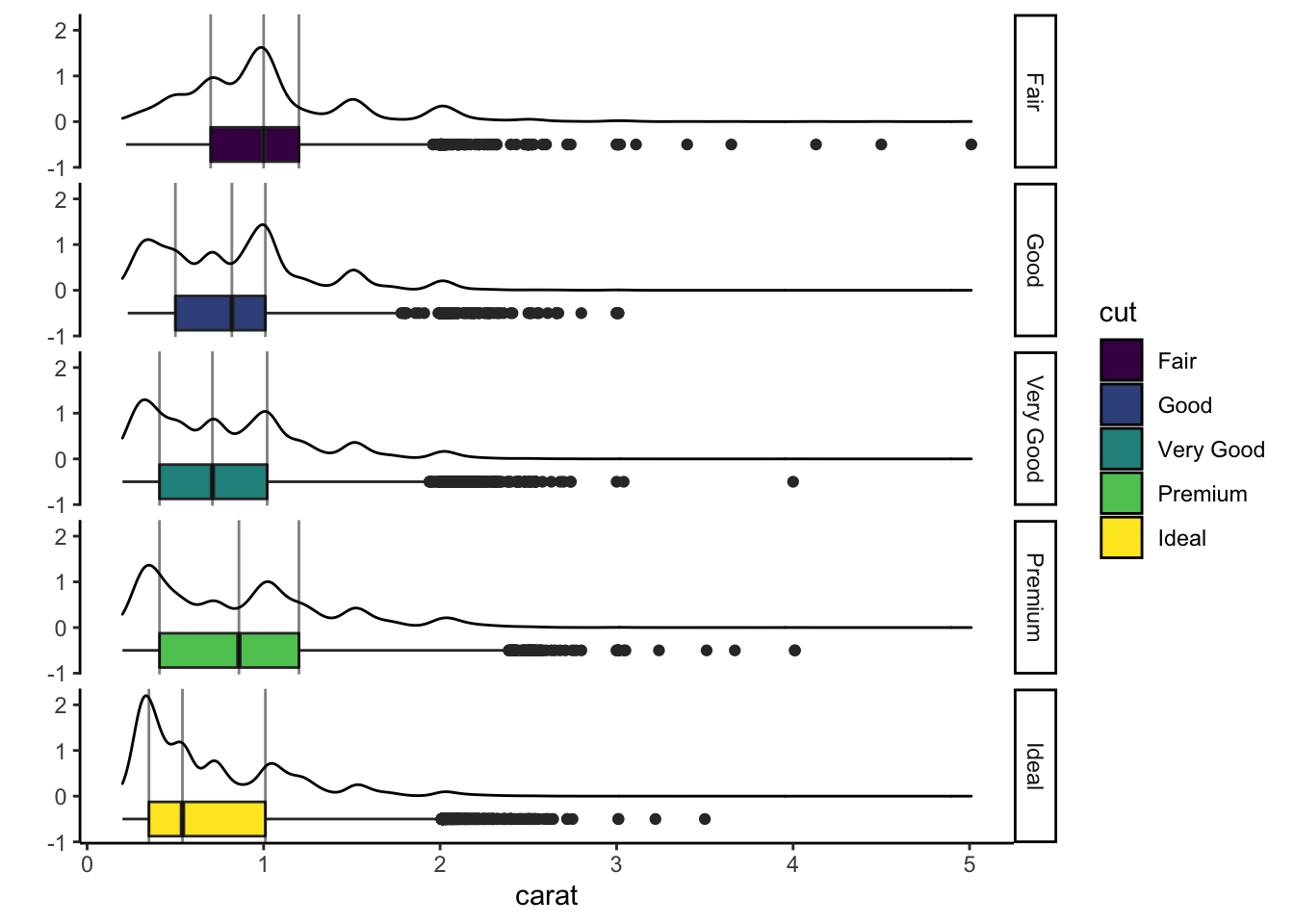
On considère les données diamonds.

Tracer les graphes suivants (utiliser coord_flip pour le second).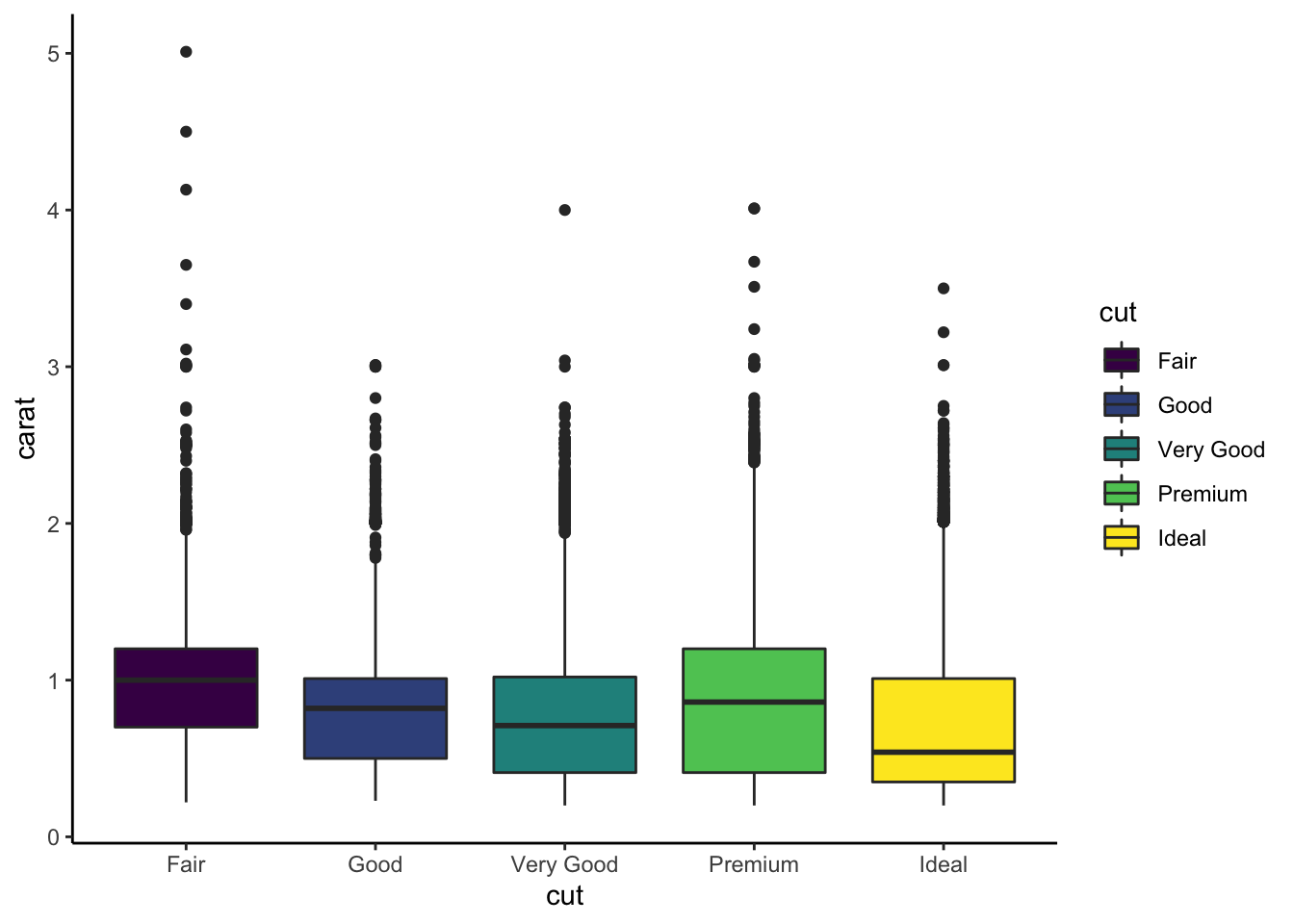
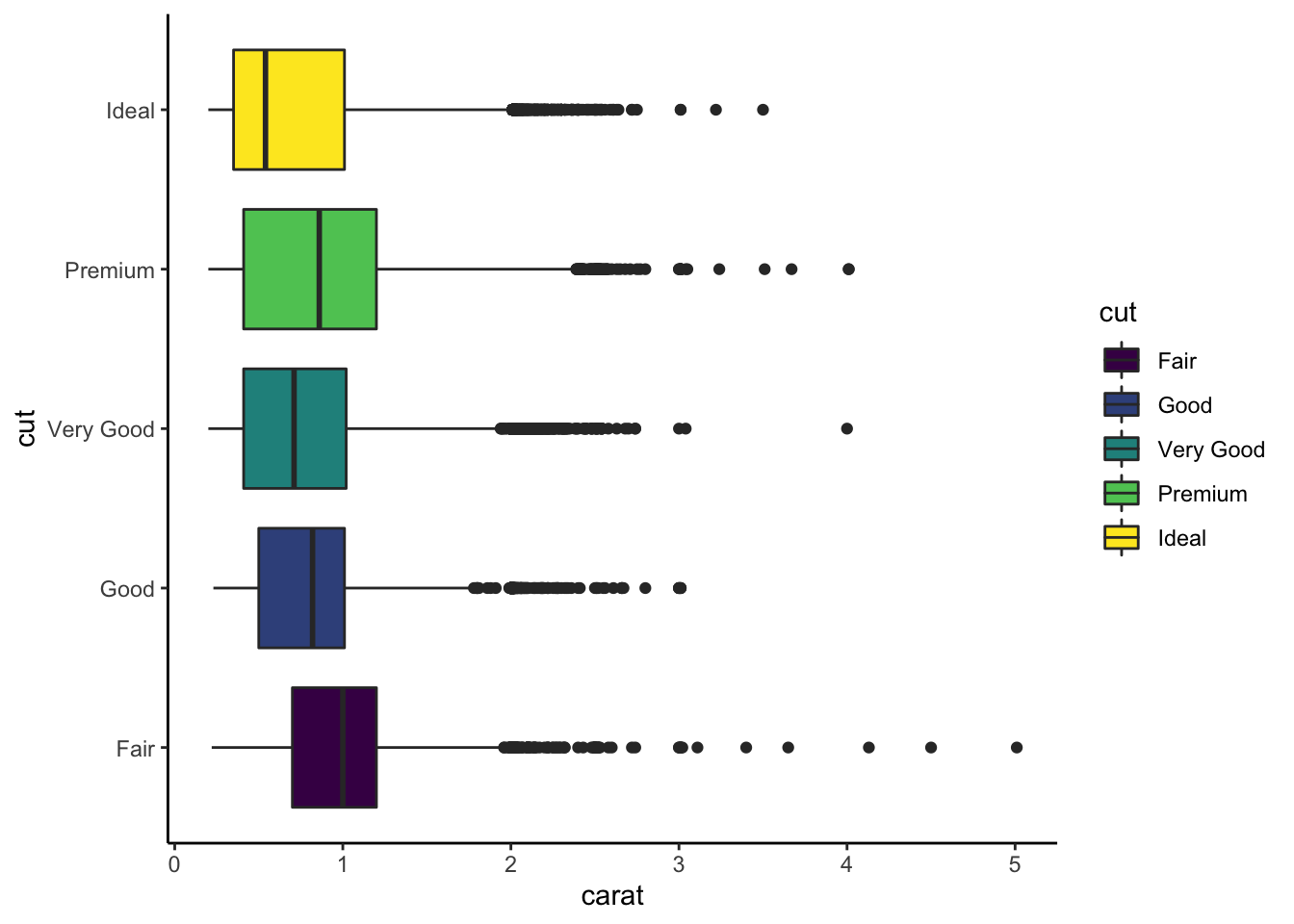
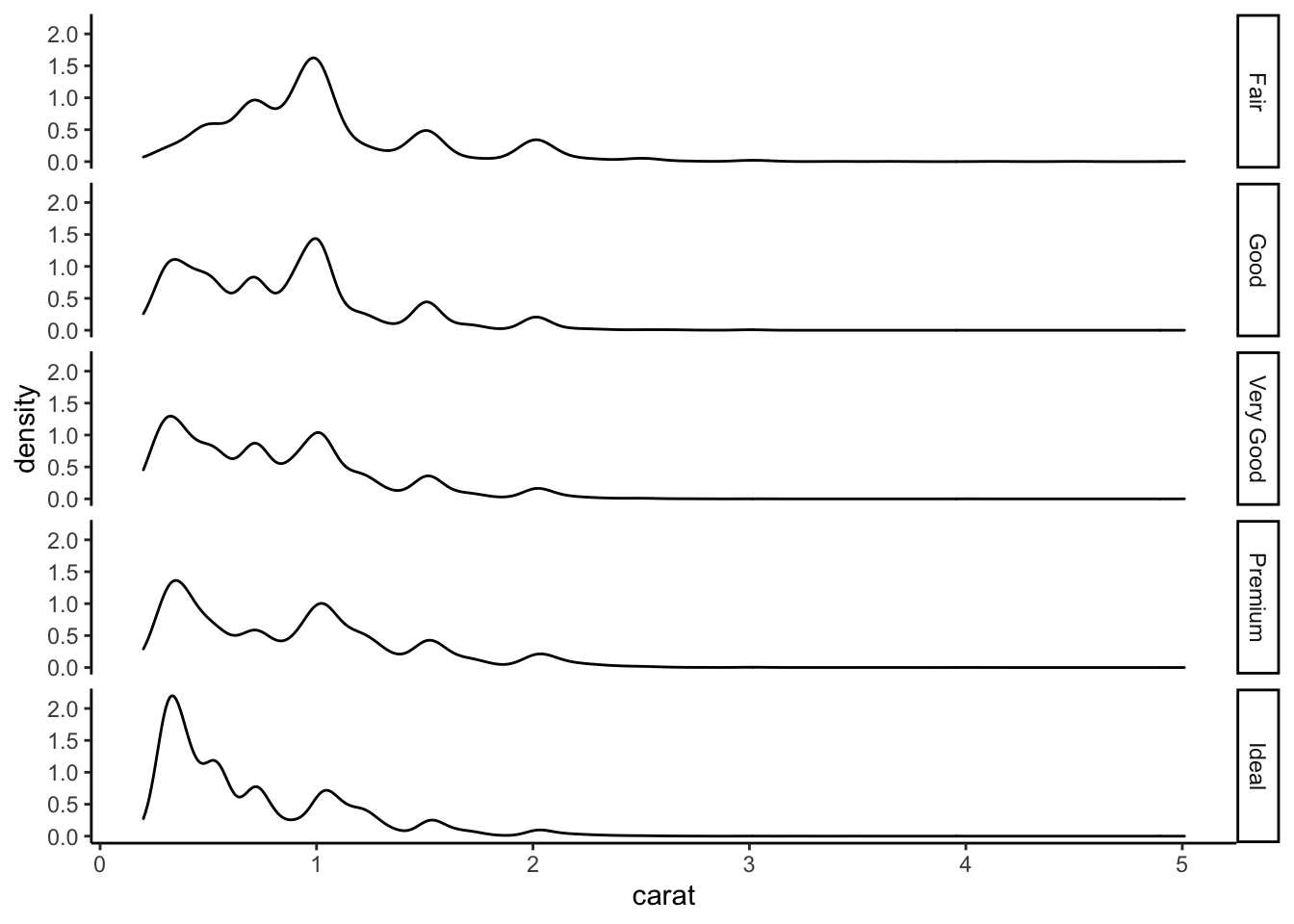
Ajouter sur le troisième graphe les quartiles de la variable carat pour chaque valeur de cut. On utilisera une ligne verticale.
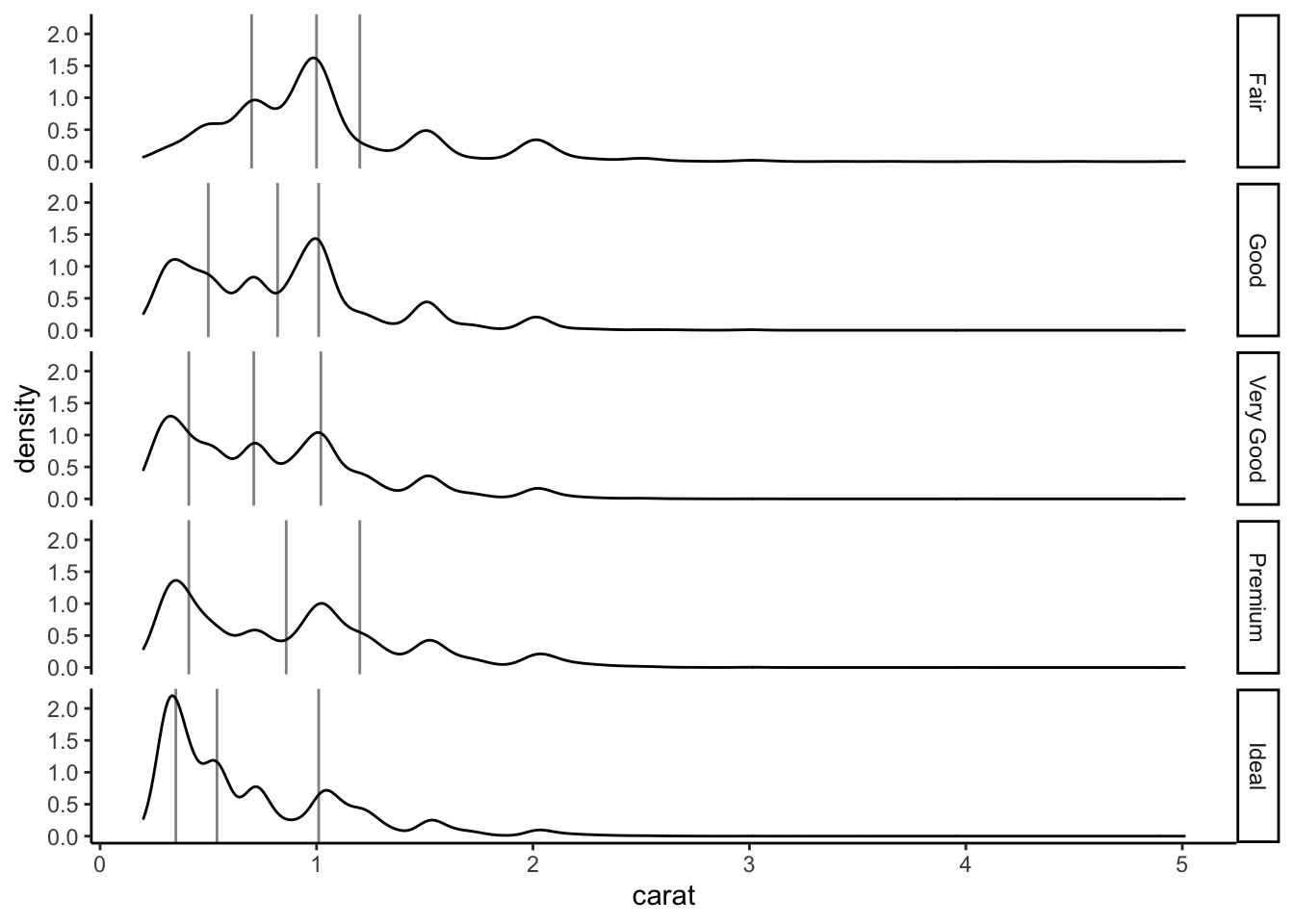
En déduire le graphe suivant (on utilisera le package ggstance).