5 Rappels sur le \(k\)-means et la CAH
Ces méthodes sont certainement les deux algorithmes les plus utilisés en apprentissage non supervisé.
L’algorithme des \(k\)-means propose de trouver un représentant pour chaque classe, appelé centroïde, en minimisant :
\[ \frac{1}{n}\sum_{i=1}^n\min_{j=1,\dots,K}\|x_i- c_j\|^2. \]
Plusieurs types d’algorithmes peuvent être utiliser pour trouver des solutions (locales) à ce problème. Une fois la solution obtenue, les clusters s’obtiennent en affectant chaque observation à son centroïde le plus proche.
Une CAH va quant à elle définir des clusters de façon récursive en agrégeant à chaqué étape les deux clusters les plus proches au sens d’une mesure de proximité à définir.
Exercice 5.1 (kmeans et CAH sur R) On considère les données
tbl <- read_delim("data/donclassif.txt",delim = ";")
ggplot(tbl)+aes(x=V1,y=V2)+geom_point()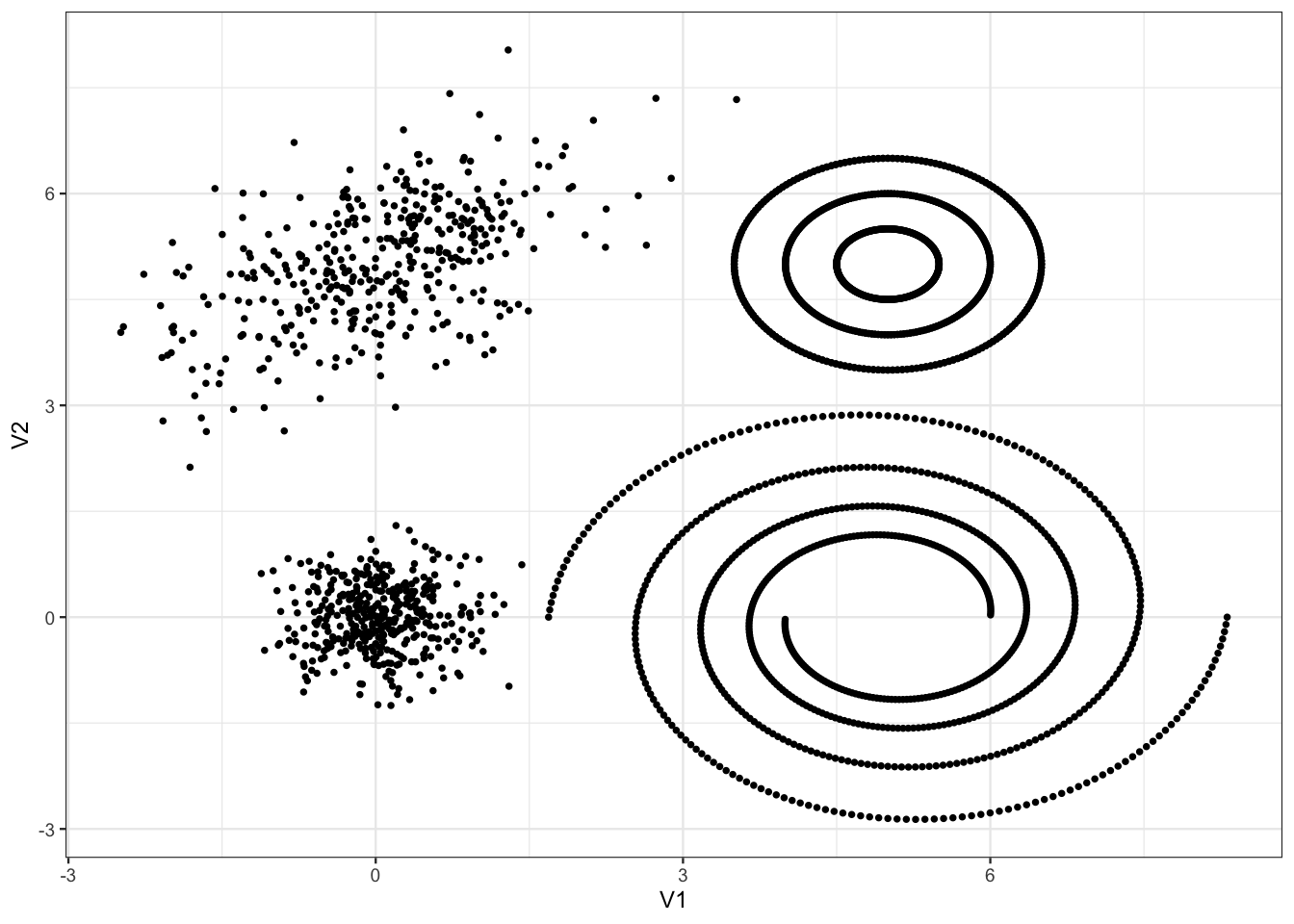
Discuter du nombre de clusters pour ce jeu de données.
Le choix du nombre de groupes est toujours une question difficile. On peut dire à minima qu’il y a 4 groupes : un dans chaque coin. Ensuite, il semble éventuellement possible de scinder les groupes de droite en sous-groupes pour arriver au total à 9-10 groupes.
Tester différents algorithmes \(k\)-means, visualiser les résultats et discuter de la capacité de cet algorithme à identifier les différentes structures géométriques des données.
Commençons par un \(k\)-means à 4 groupes :
res4 <- kmeans(tbl,centers = 4,nstart = 100) tbl1 <- tbl |> mutate(`K=4`=res4$cluster) ggplot(tbl1)+aes(x=V1,y=V2,color=as.factor(`K=4`))+ geom_point()+labs(color="K=4")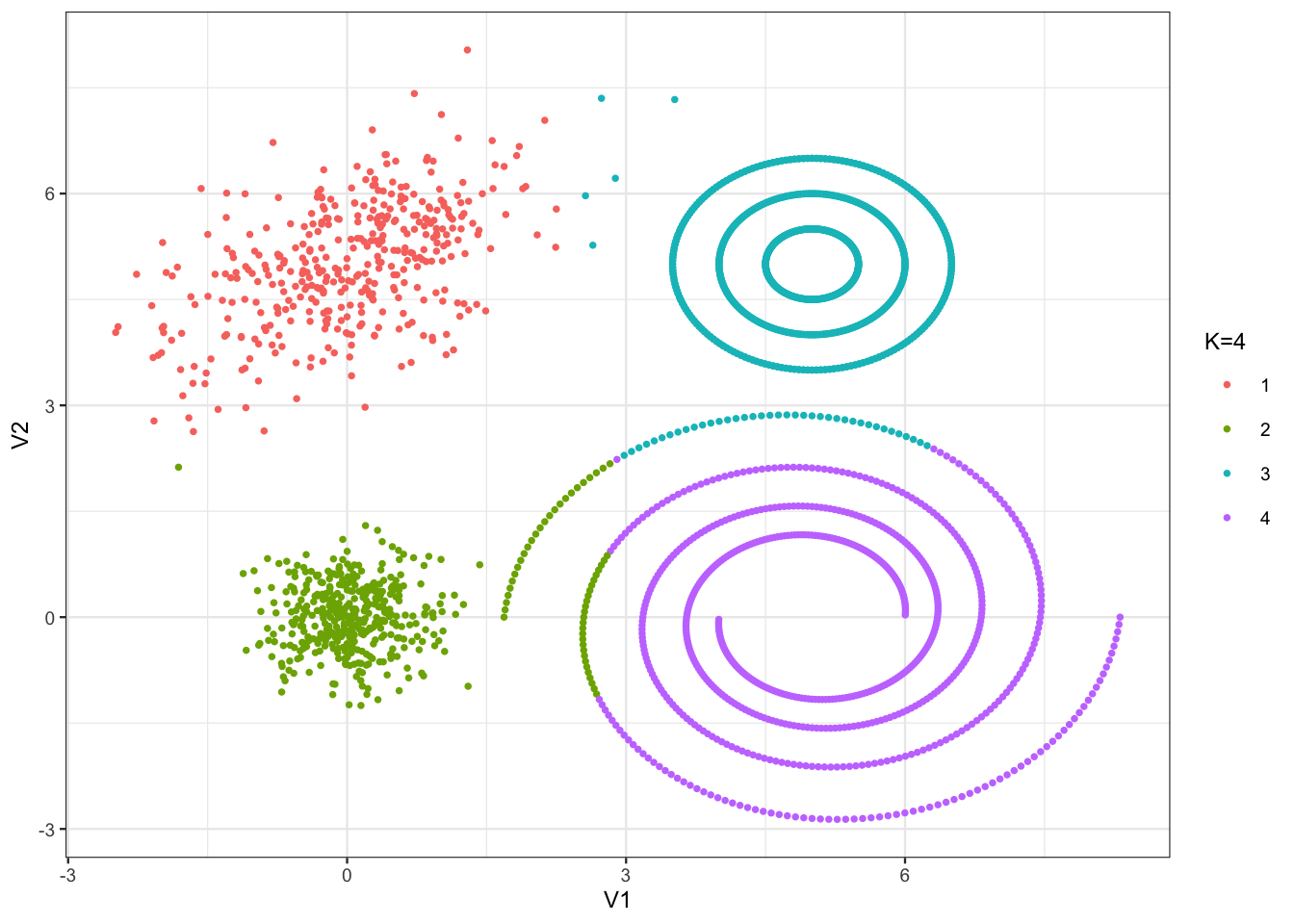
On passe à plus de groupes
nom <- paste("K=",5:9,sep="") mat <- matrix(0,ncol=5,nrow=nrow(tbl)) k <- 5:9 for (j in 1:5){ res <- kmeans(tbl,centers = k[j],nstart = 100) mat[,j] <- res$cluster } mat1 <- as_tibble(mat) names(mat1) <- nom (tbl2 <- tbl1 |> bind_cols(mat1))# A tibble: 2,800 × 8 V1 V2 `K=4` `K=5` `K=6` `K=7` `K=8` `K=9` <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> 1 6.00 0.0315 4 4 6 3 5 4 2 6.00 0.0632 4 4 6 3 5 4 3 6.00 0.0950 4 4 6 3 5 4 4 6.00 0.127 4 4 6 3 5 4 5 6.00 0.159 4 4 6 3 5 4 6 6.00 0.191 4 4 6 3 5 4 7 6.00 0.223 4 4 6 3 5 4 8 5.99 0.255 4 3 6 3 5 4 9 5.99 0.287 4 3 6 3 5 4 10 5.98 0.318 4 3 6 3 5 4 # ℹ 2,790 more rowsOn visualise les résultats :
tbl3 <- tbl2 |> pivot_longer(-c(V1,V2),names_to = "Nb_clust",values_to="groupes") |> mutate(groupes=as.factor(groupes)) ggplot(tbl3)+aes(x=V1,y=V2,color=groupes)+ geom_point()+facet_wrap(~Nb_clust)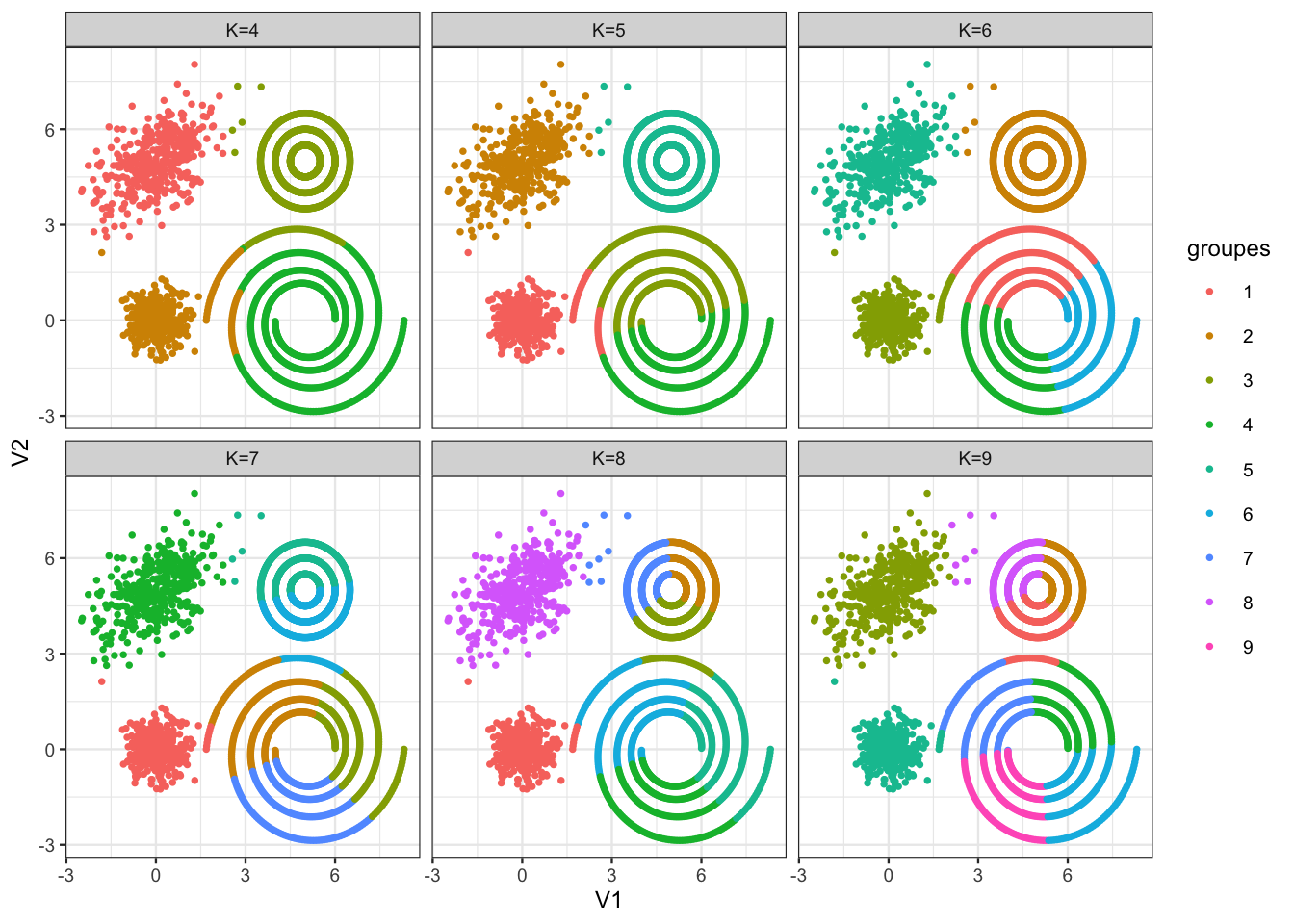
Sans surprise, le \(k\)-means ne parvient pas à scinder les spirales en bas à droite et les cercles concentriques en haut à droite.
Sélectionner le nombre de classes à l’aide du coefficient de silhouette. On pourra utiliser la fonction
fviz_nbclustdu package factoextra. Visualiser les clusters avecfviz_cluster.library(factoextra) fviz_nbclust(tbl, kmeans, method = "silhouette")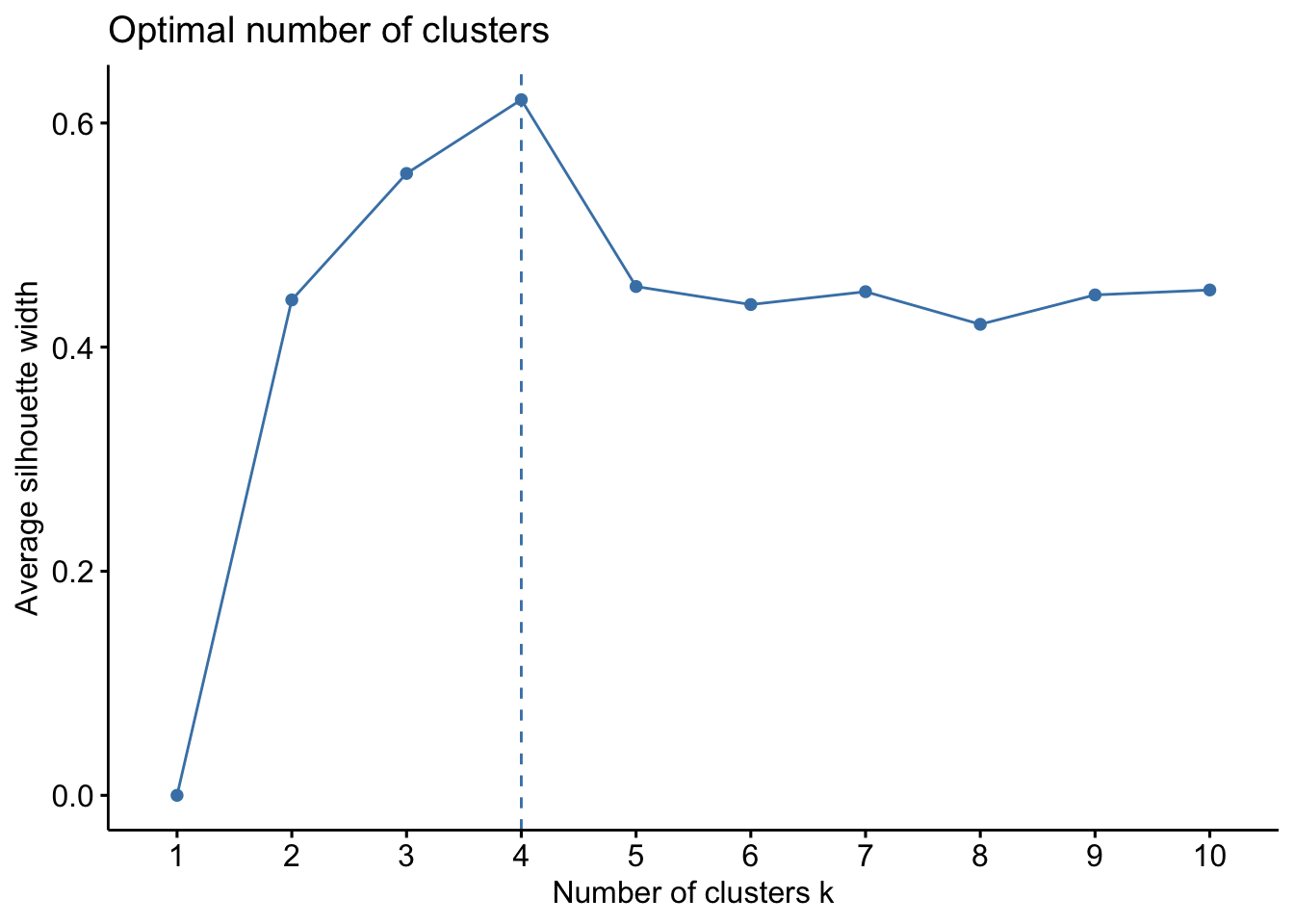
On choisit 4 groupes que l’on visualise :
res4 <- kmeans(tbl,centers = 4,nstart = 100) fviz_cluster(res4,tbl,ellipse = FALSE,labelsize = 0)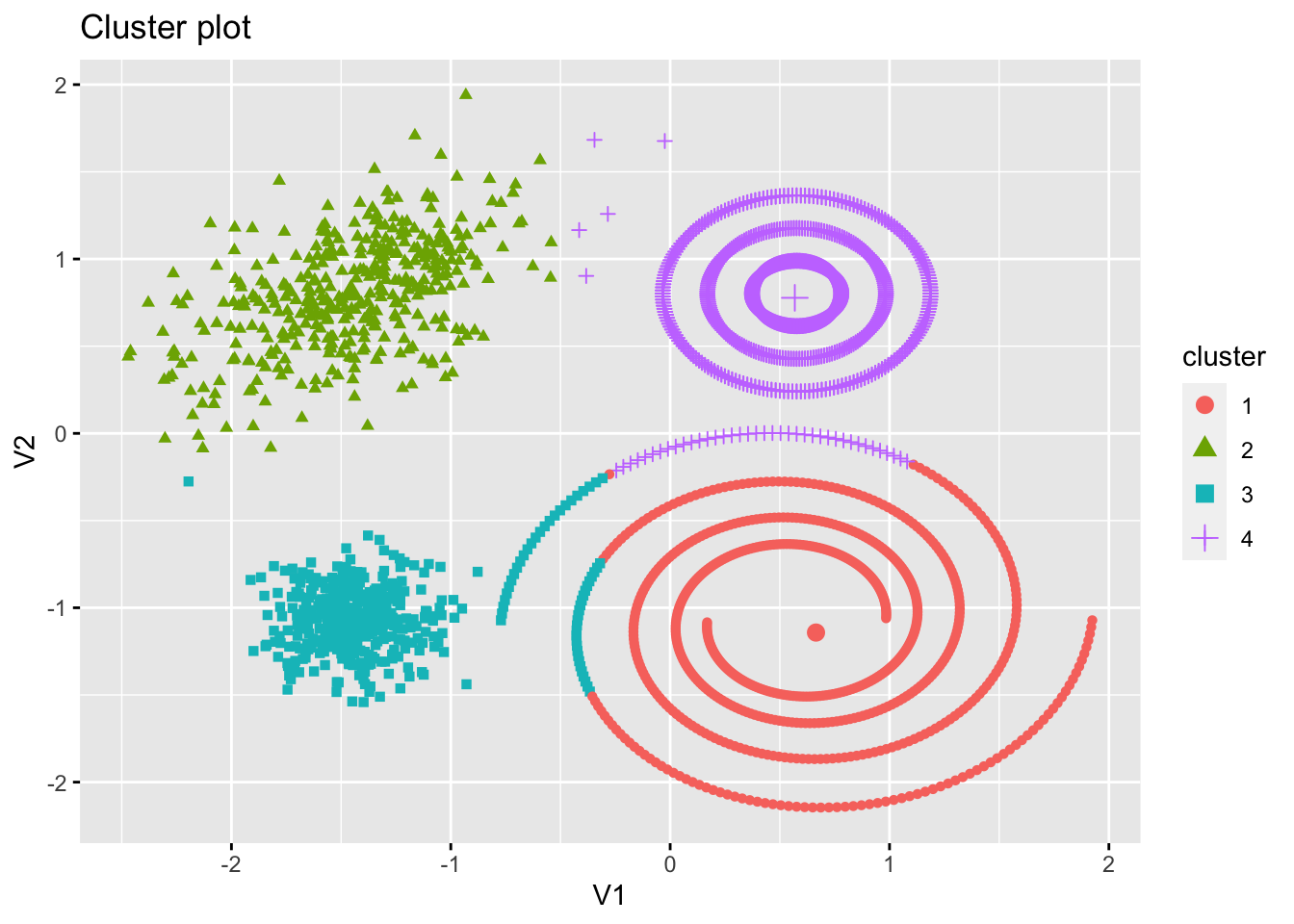
Faire le même travail avec la classification ascendente hiérarchique. On commencera par comparer les différentes méthodes d’agglomération en fonction du nombre de clusters, afin d’en déduire une stratégie efficace permettant notamment d’identifier les spirales et les cercles concentriques.
On commence par calculer la matrice de distances et on visualise les dendrogrammes
DD <- dist(tbl) ward <- hclust(DD,method="ward.D2") single <- hclust(DD,method="single") complete <- hclust(DD,method="complete") average <- hclust(DD,method="average")library(ggdendro) ggdendrogram(ward)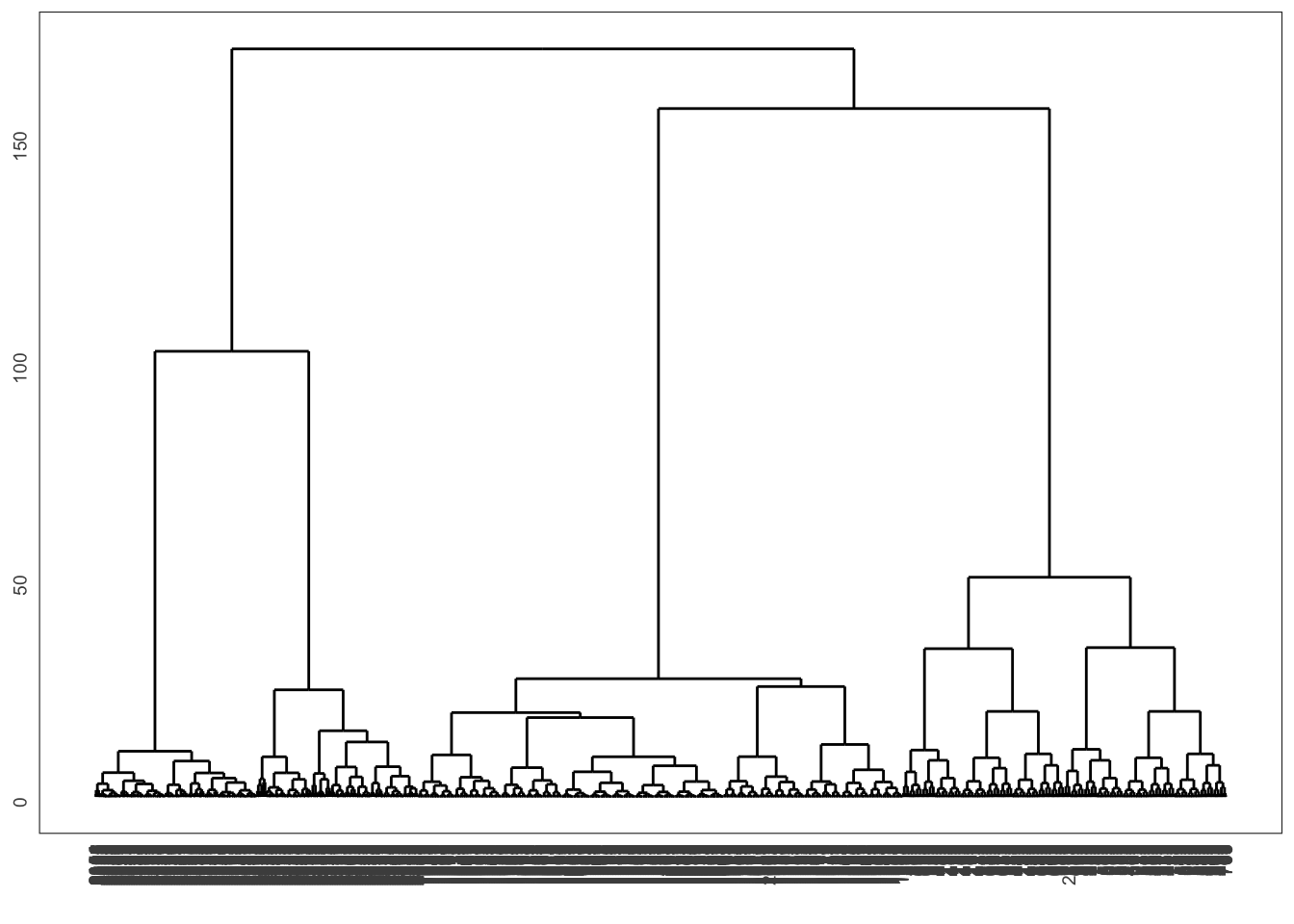
ggdendrogram(single)
ggdendrogram(complete)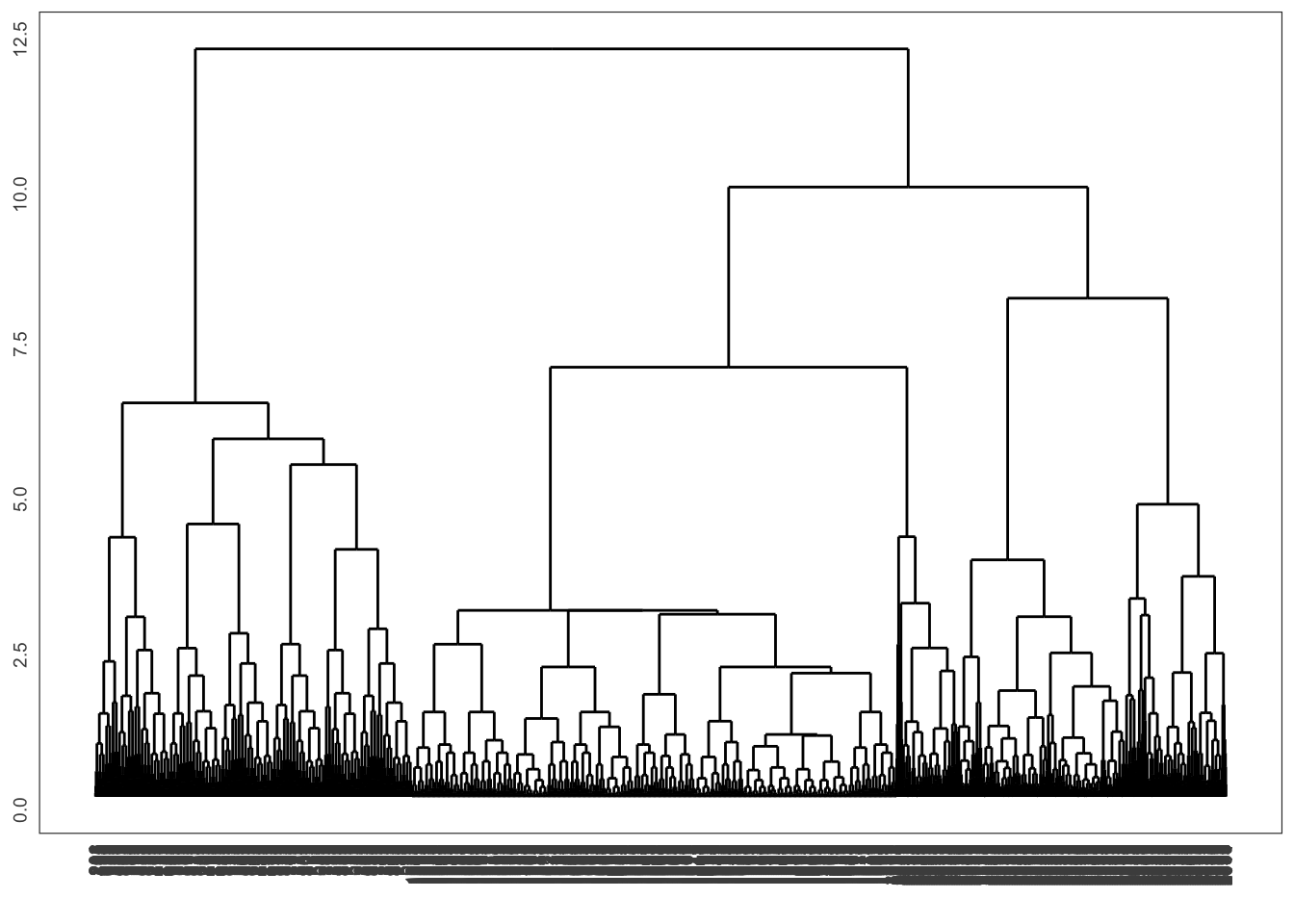
ggdendrogram(average)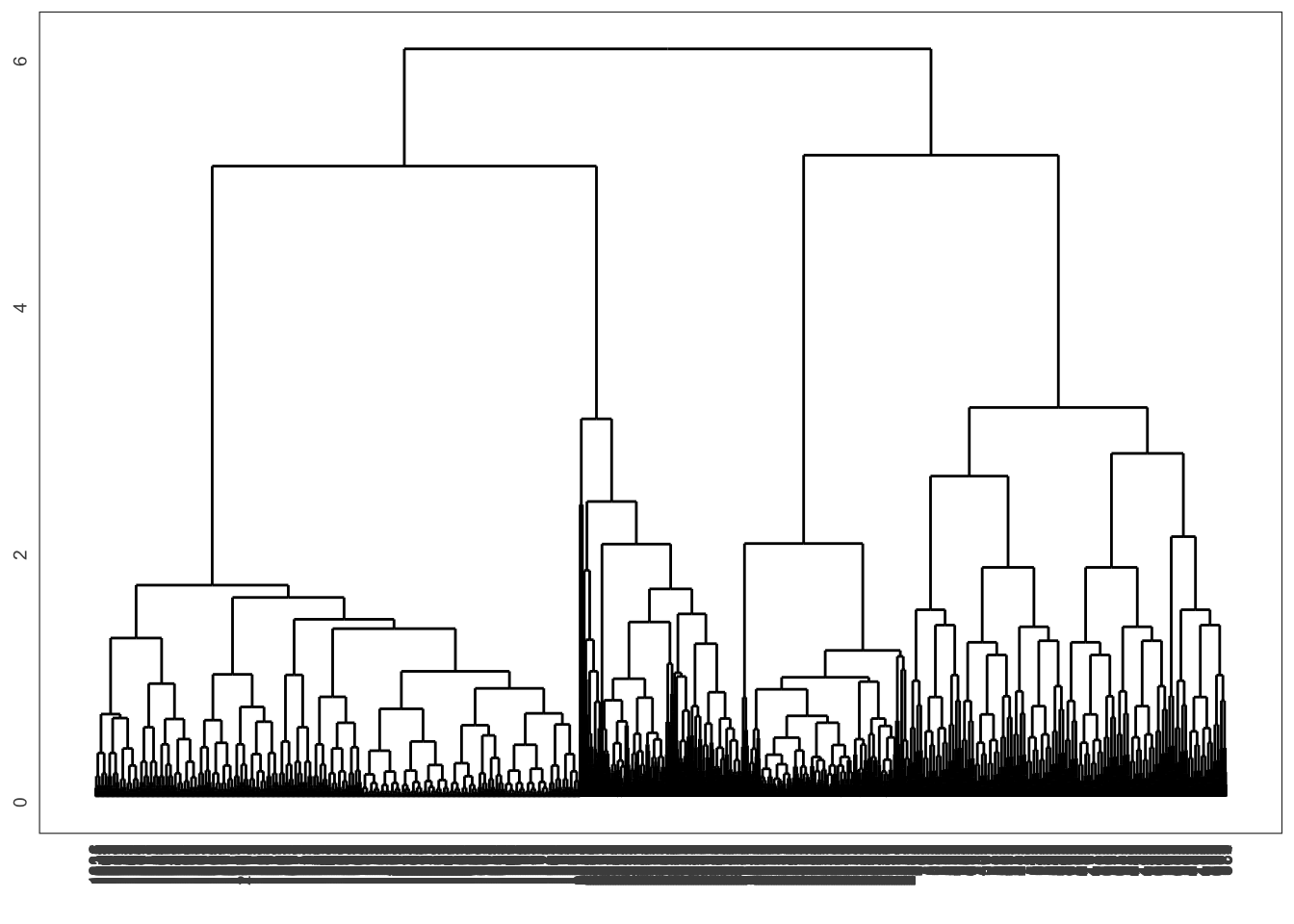
On regarde maintenant ce qu’il se passe pour un nombre de classes fixé, par exemple 8.
ward8 <- cutree(ward,k = 8) single8 <- cutree(single,k = 8) complete8 <- cutree(complete,k = 8) average8 <- cutree(average,k = 8) tbl_cah <- tbl |> mutate( ward = ward8, single = single8, complete = complete8, average = average8) tbl1_cah <- tbl_cah |> pivot_longer(-c(V1, V2), names_to = "Nb_clust", values_to = "groupes") |> mutate(groupes = as.factor(groupes)) ggplot(tbl1_cah) + aes(x = V1, y = V2, color = groupes) + geom_point() + facet_wrap(~ Nb_clust)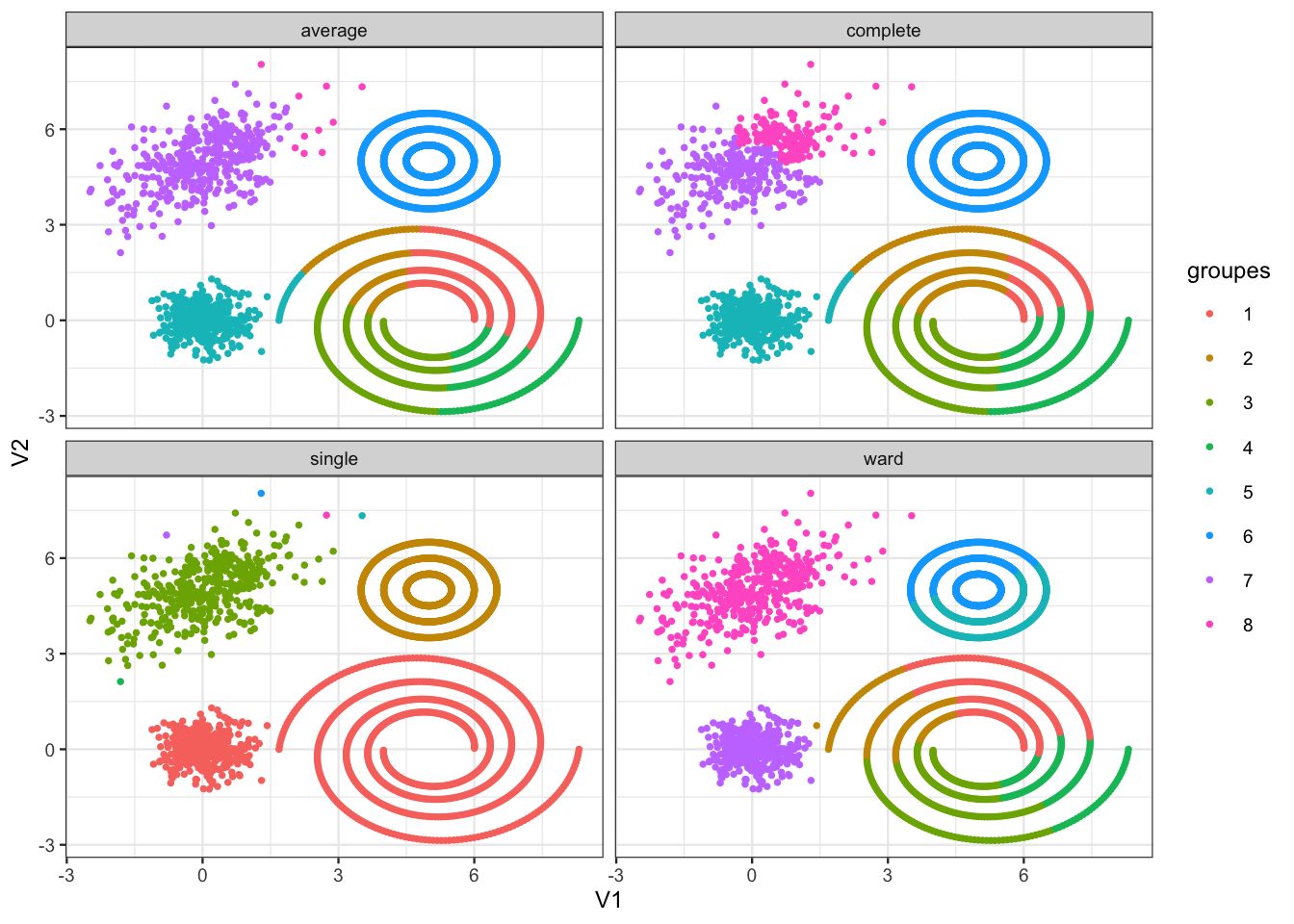
Ici encore il est difficile d’identifier les cercles concentriques et la spirale. Pour y parvenir, on propose de regarder un peu plus en détails le lien simple :
fviz_nbclust(tbl, hcut, method = "silhouette", hc_method="single", k.max=50)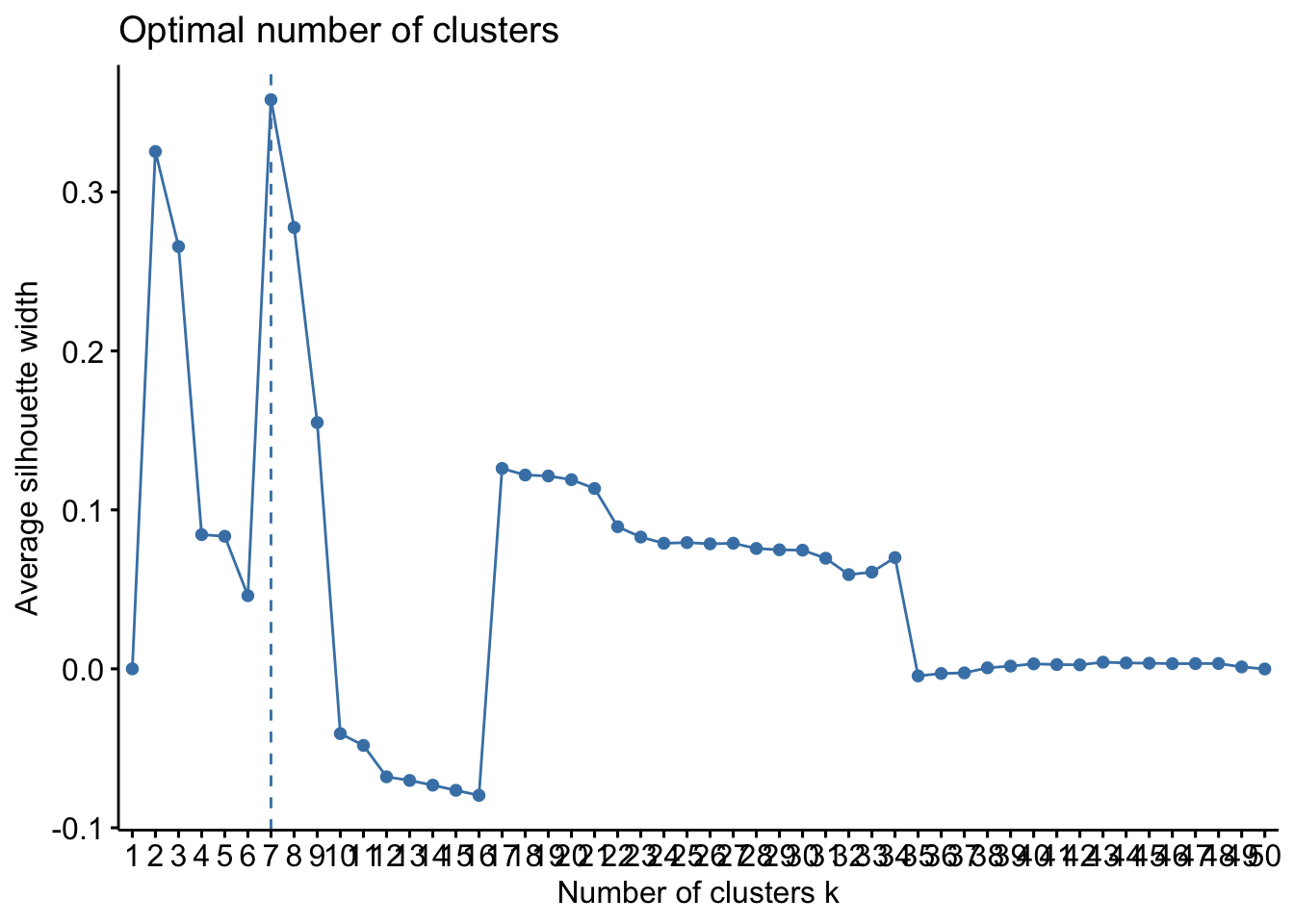
La silouhette augmente à nouveau quand on passe à 17 groupes : cela correspond à la division des groupes du bas :
single16 <- cutree(single,k = 16) single17 <- cutree(single,k = 17) tbl |> mutate(`G=16`=single16,`G=17`=single17) |> pivot_longer(-c(V1, V2), names_to = "Nb_clust", values_to = "groupes") |> mutate(groupes = as.factor(groupes)) |> ggplot() + aes(x = V1, y = V2,color = groupes) + geom_point() + facet_wrap(~ Nb_clust)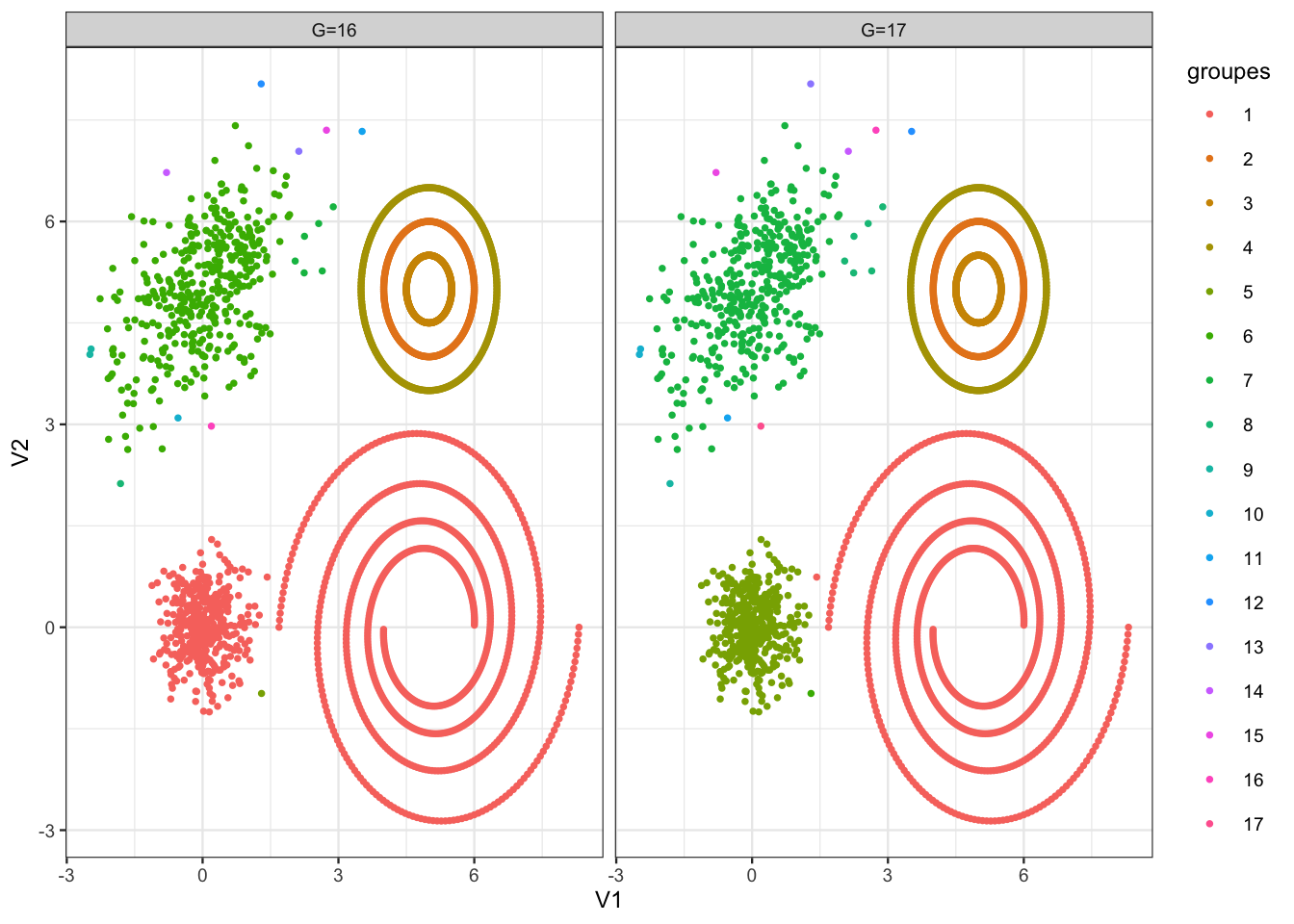
On a également une cassure lorsqu’on passe à 35 groupes avec ici une baisse de la silouhette :
single34 <- cutree(single,k = 34) single35 <- cutree(single,k = 35) tbl |> mutate(`G=34`=single34,`G=35`=single35) |> filter(`G=35`<=2) |> pivot_longer(-c(V1, V2), names_to = "Nb_clust", values_to = "groupes") |> mutate(groupes = as.factor(groupes)) |> ggplot() + aes(x = V1, y = V2,color = groupes) + geom_point() + facet_wrap(~ Nb_clust)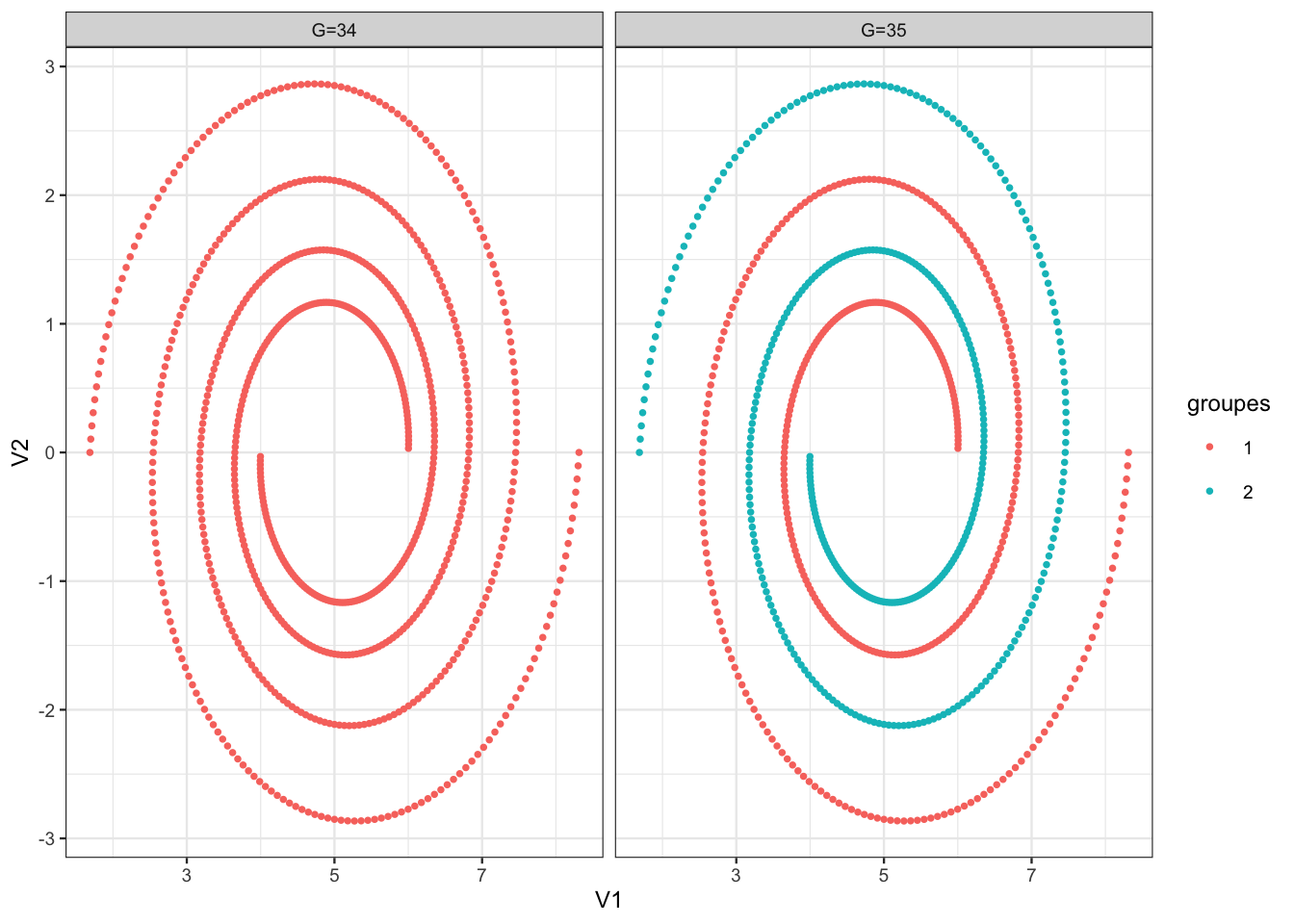
Elle provient de la séparation des spirales. L’identification des spirales produit donc une baisse de la silouhette. Cela s’explique par le fait que ce coefficient n’est pas adapté à ce type de structures géométriques (il va privilégier des clusters à géométrie sphérique). On termine en visualisant la classification à 35 groupes, en ne conservant que les “gros” groupes :
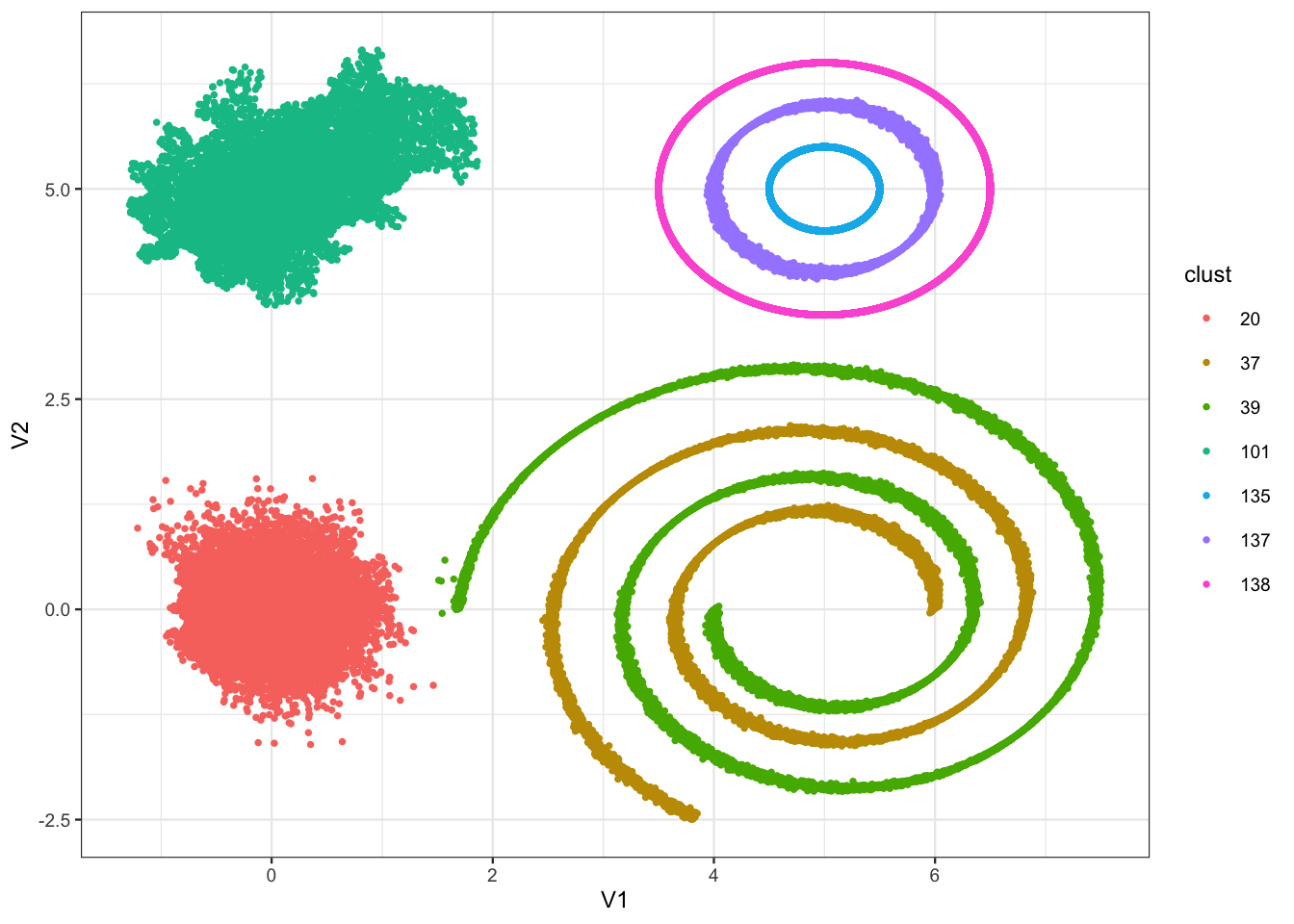
table(single35)single35 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 400 400 400 400 400 398 1 1 349 1 1 1 4 20 2 1 1 2 1 1 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1keep_groupe <- which(table(single35)>=100) tbl |> mutate(single35=single35) |> filter(single35 %in% keep_groupe) |> mutate(single35=as.factor(single35)) |> ggplot()+aes(x = V1, y = V2,color = single35) + geom_point()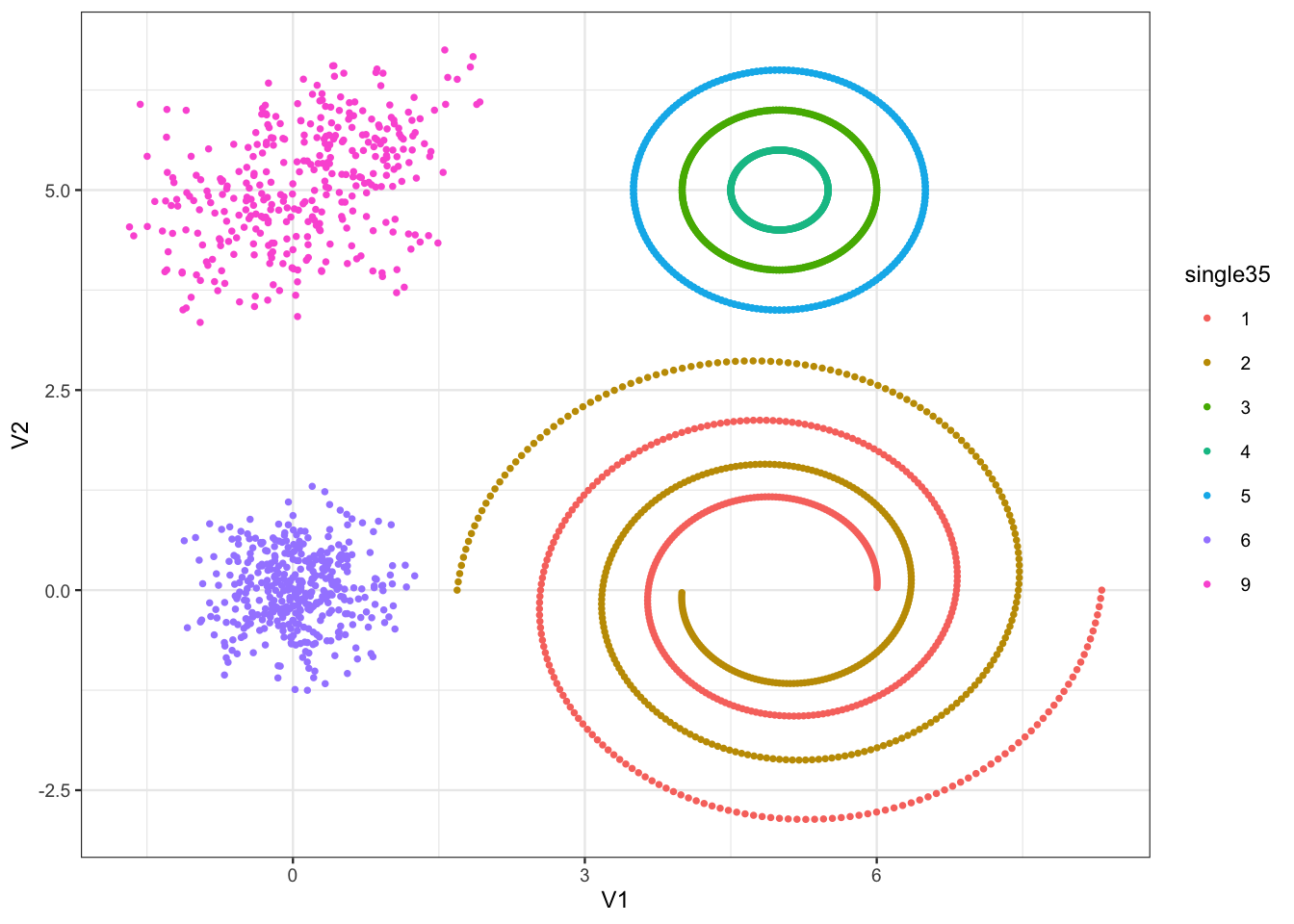
Exercice 5.2 (CAH sur un gros jeu de données) On reprend le même jeu de données mais avec plus d’individus :
tbl <- read_delim("data/donclassif2.txt",delim = ";")
dim(tbl)[1] 70000 2Que se passe t-il lorsque vous faites une CAH ?
DD <- dist(tbl)Error: vector memory exhausted (limit reached?)Le nombre d’individus est trop important pour calculer la matrice des distances. Il est bien connu qu’on ne peut pas faire une CAH lorsque \(n\) est (trop) grand.
Proposer une solution pour faire quand même la CAH.
La solution classique consiste à faire une classification mixte :
- Faire un \(k\)-means avec un nombre de groupes conséquent ;
- Faire le CAH sur les centroïdes du \(k\)-means (en prenant en compte la taille des clusters). Sur
Sur R on peut faire cela avec la fonction
HCPCdu packageFactoMineR.library(FactoMineR) classif <- HCPC(tbl,kk=2000,nb.clust = 150, method="single", description = FALSE,graph = FALSE) keep_groupe <- which(table(classif$data.clust$clust)>1000) as_tibble(classif$data.clust) |> filter(clust%in%keep_groupe) |> ggplot() + aes(x=V1,y=V2,color=clust)+geom_point()