2  Forêts aléatoires

Les méthodes par arbres présentées précédemment sont des algorithmes qui possèdent tout un tas de qualités (facile à mettre en œuvre, interprétable…). Ce sont néanmoins rarement les algorithmes qui se révèlent les plus performants. Les méthodes d’agrégation d’arbres présentées dans cette partie sont souvent beaucoup plus pertinentes, notamment en terme de qualité de prédiction. Elles consistent à construire un très grand nombre d’arbres “simples” : \(g_1,\dots,g_B\) et à les agréger en faisant la moyenne : \[\frac{1}{B}\sum_{k=1}^Bg_k(x).\] Les forêts aléatoires (Breiman 2001) et le gradient boosting (Friedman 2001) utilisent ce procédé d’agrégation. Dans ce chapitre on étudiera ces algorithmes sur le je de données spam :

library(kernlab)
data(spam)
set.seed(1234)
spam <- spam[sample(nrow(spam)),]

Le problème est d’expliquer la variable binaire type par les autres.

L’algorithme des forêts aléatoires consiste à construire des arbres sur des échantillons bootstrap et à les agréger. Il peut s’écrire de la façon suivante :

Entrées :

• \(x\in\mathbb R^d\) l’observation à prévoir, \(\mathcal D_n\) l’échantillon ;
• \(B\) nombre d’arbres ; \(n_{max}\) nombre max d’observations par nœud
• \(m\in\{1,\dots,d\}\) le nombre de variables candidates pour découper un nœud.

Algorithme : pour \(k=1,\dots,B\) :

1. Tirer un échantillon bootstrap dans \(\mathcal D_n\)
2. Construire un arbre CART sur cet échantillon bootstrap, chaque coupure est sélectionnée en minimisant la fonction de coût de CART sur un ensemble de \(m\) variables choisies au hasard parmi les \(d\). On note \(T(.,\theta_k,\mathcal D_n)\) l’arbre construit.

Sortie : l’estimateur \(T_B(x)=\frac{1}{B}\sum_{k=1}^BT(x,\theta_k,\mathcal D_n)\).

Cet algorithme peut être utilisé sur R avec la fonction randomForest du package randomForest ou la fonction ranger du package ranger.

Exercice 2.1 (Biais et variance des algorithmes bagging) Comparer le biais et la variance de la forêt \(T_B(x)\) au biais et à la variance d’un arbre de la forêt \(T(x,\theta_k,\mathcal D_n)\). On pourra utiliser \(\rho(x)=\text{corr}(T(x,\theta_1,\mathcal D_n),T(x,\theta_2,\mathcal D_n))\) pour comparer les variances.

Pour simplifier les notations on considère \(T_1,\dots,T_B\) \(B\) variables aléatoires de même loi et de variance \(\sigma^2\). Il est facile de voir que \(\mathbf E[\bar T]=\mathbf E[T_1]\). Pour la variance on a

\[ \begin{aligned} \mathbf V[\bar T]= & \frac{1}{B^2}\mathbf V\left[\sum_{i=1}^BT_i\right]= \frac{1}{B^2}\left[\sum_{i=1}^V\mathbf V[T_i]+\sum_{i\neq j}\mathbf{cov}(T_i,T_j)\right] \\ = & \frac{1}{B^2}\left[B\sigma^2+B(B-1)\rho\sigma^2\right]=\rho\sigma^2+\frac{1-\rho}{B}\sigma^2. \end{aligned} \]

Considérons \(\rho\leq 0\). On déduit de l’équation précédente que \(B\leq 1-1/\rho\). Par exemple si \(\rho=-1\), \(B\) doit être inférieur ou égal à 2. Il n’est en effet pas possible de considérer 3 variables aléatoires de même loi dont les corrélations 2 à 2 sont égales à -1. De même si \(\rho=-1/2\), \(B\leq 3\)…

Exercice 2.2 (RandomForest versus ranger) On sépare le jeu de données spam en un échantillon d’apprentissage et un échantillon test :

set.seed(1234)
library(tidymodels)
data_split <- initial_split(spam, prop = 3/4)
spam.app <- training(data_split)
spam.test  <- testing(data_split)

1. Entraîner une forêt aléatoire sur les données d’apprentissage uniquement en utilisant les paramètres par défaut de la fonction randomForest. Commenter.

   Il s’agit d’une forêt de classification avec 500 arbres. Le paramètre mtry vaut 7 et l’erreur OOB est de 4.72%.

2. Calculer les groupes prédits pour les individus de l’échantillon test et en déduire une estimation de l’erreur de classification.

3. Calculer les estimations de la probabilité de spam pour les individus de l’échantillon test.

4. Refaire les questions précédentes avec la fonction ranger du package ranger (voir https://arxiv.org/pdf/1508.04409.pdf).

   library(ranger)

   Si on souhaite estimer les probabilités d’être (ou pas) spam, il faut le spécifier dans la construction de la forêt :

5. Comparer les temps de calcul de randomForest et ranger.

   ranger est beaucoup plus rapide.

Exercice 2.3 (Sélection des paramètres) Nous nous intéressons ici au choix des paramètres de la forêt aléatoire.

1. Expliquer la sortie suivante.

   set.seed(12345)
   library(OOBCurve)
   foret1 <- ranger(type~.,data=spam,keep.inbag=TRUE)
   spam.task <- mlr::makeClassifTask(data=spam,target="type")
   erreurs <- OOBCurve(foret1,measures = list(mmce, auc),
                   task=spam.task,data=spam)
   erreurs1 <- erreurs |> as_tibble() |> mutate(ntrees=1:500) |> 
     filter(ntrees>=5) |>
     pivot_longer(-ntrees,names_to="Erreur",values_to="valeur")  
   ggplot(erreurs1)+aes(x=ntrees,y=valeur)+geom_line()+
     facet_wrap(~Erreur,scales="free")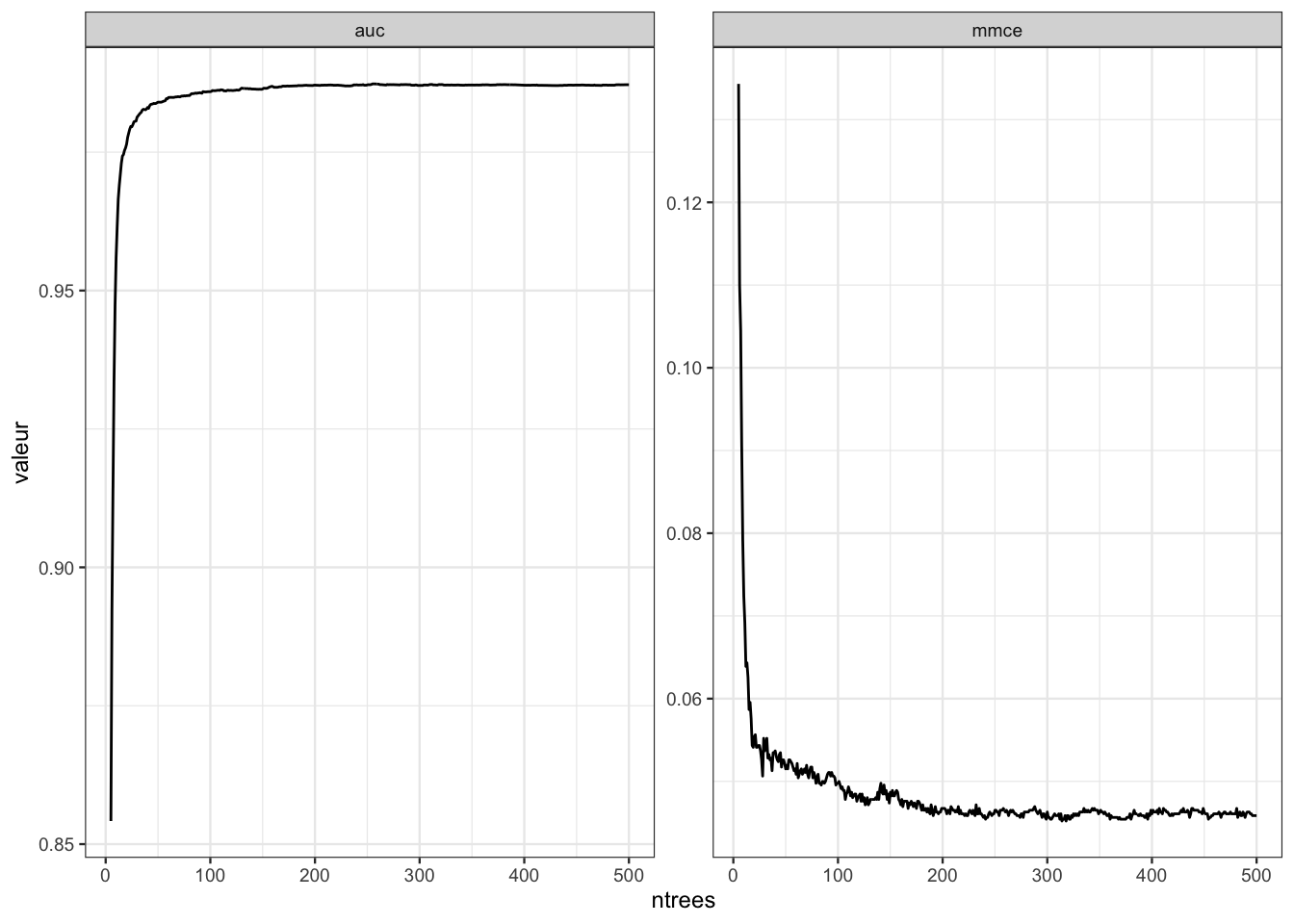

   

   Ce graphe permet de visualiser l’évolution des erreurs OOB (AUC et erreur de classification) en fonction du nombre d’arbres. Il peut être utilisé pour voir si l’algorithme a bien “convergé”. Si ce n’est pas le cas, il faut construire une forêt avec plus d’arbres.

2. Construire la forêt avec mtry=1 et comparer ses performances avec celle construite précédemment.

   La forêt foret1 est plus performante en terme d’erreur de classification OOB.

3. A l’aide des outils tidymodels sélectionner les paramètres mtry et min_n dans les grilles c(1,6,seq(10,50,by=10),57) et c(1,5,100,500). On pourra notamment visualiser les critères en fonction des valeurs de paramètres.

   On commence par construire la grille :

   On définit le workflow

   On effectue la validation croisée en parallélisant :

   On étudie les meilleures valeurs de paramètres pour les deux critères considérés :

   On visualise les erreurs de classification

   et les AUC

   On retrouve bien des petites valeurs pour min_n : il faut des arbres profonds pour que la forêt soit performante. Les valeurs optimales de mtry se situent autours de la valeur par défaut (7 ici). On peut donc conserver cette valeur pour ré-ajuster la forêt sur toutes les données :

4. Visualiser l’importance des variables pour les scores d’impureté et de permutations.

Exercice 2.4 (Arbre vs forêt aléatoire) Proposer et mettre en œuvre une procédure permettant de comparer les performances (courbes ROC, AUC et accuracy) d’un arbre CART utilisant la procédure d’élagage proposée dans la Section 1.2 avec une forêt aléatoire.

On peut envisager différentes stratégies pour répondre à cette question. Il convient de bien préciser ce que l’on souhaite faire. Il ne s’agit pas de sélectionner les paramètres d’un algorithme. On souhaite comparer deux algorithmes de prévision :

• un arbre CART qui utilise la procédure d’élagage CART : création de la suite optimale de sous arbre puis sélection d’un arbre dans cette suite en estimant l’erreur de classification par validation croisée ;
• une forêt aléatoire qui prend les valeurs par défaut pour nodesize et qui sélection mtry en minimisant l’erreur OOB (c’est un choix).

Il faut estimer les risques demandés en se donnant une stratégie de ré-échantillonnage. On choisit une validation croisée 10 blocs :

On crée une fonction spécifique à chaque algorithme qui calculera les prévisions de nouveaux individus :

On effectue la validation croisée :

On déduit la courbe ROC, l’AUC

et l’accuracy

Breiman, L. 2001. « Random forests ». Machine learning 45: 5‑32.

Friedman, J. H. 2001. « Greedy Function Approximation: A Gradient Boosting Machine ». Annals of Statistics 29: 1189‑1232.